okrag tomcio: Na OX wynzaczyć punkt, by styczne poprowadzone z tego punktu do okręgów x2+y2=6y−6, x2+y2=2x były równej dlugości. bardzo proszę o pomoc , rozwiązanie wraz z wyjaśnieniem

Basia: styczne to proste; długość każdej prostej = +∞ napisz więc porządnie o co chodzi

tomcio: tak brzmi cale zadania i tam gdzie są okręgi x²+y²=6y−6 x²+y²=2x

tomcio: moim zdaniem chodzi o punkt gdzie promień pada na styczną prostopadle.

tomcio: w sensie chodzi chyba o odległośc z OX na owy punkt

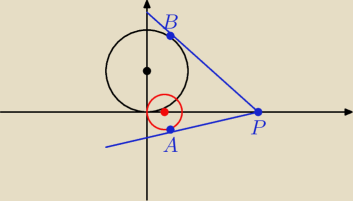
Basia: PA = PB o to chodzi ?

tomcio: tak.

kruk: tylko nie zapominajcie, że te okręgi nie nachodzą na siebie i , że wynikiem będą dwa punkty na OX

Basia: niech P(x₀, 0) proste k i l przechodzące przez P mają równanie y = ax+b 0 = ax₀+b b = −ax₀ k: y = ax − ax₀ = a(x−x₀) l: y = ax − ax₀ = a(x−x₀) teraz należałoby zbadać jakie warunki muszą być spełnione aby k była styczna do pierwszego, a l do drugiego okręgu nie dostaniemy konkretnych wartości tylko związek między parametrami a i x₀ pozbywamy się jednego parametru i szukamy teraz punktów wspólnych czyli A, B nadal to będą wyniki z parametrem potem warunek: |AP|² = |BP|² strasznie żmudne rachunki to będą, ale chyba wykonalne −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− może jest jakiś prostszy sposób trzeba jeszcze pomyśleć

Basia: @kruk nieprawda, to są okręgi przecinające się S₁(0,3) r₁=3 S₂(1,0) r₂=1

tomcio: dzięki, przynajmnije wiem od czego zacząć

kruk: w tym pierwszym masz: a=0 b=3 c=6 6=0²+3²−r² 6=9−r² r²=3 r=√3

Basia: poprawka: r₁ = √3 S₁S₂ = √10 r₁+r₂ = √3+1 rzeczywiście nie mają punktów wspólnych

papanoe: S1S2 = 3 S1=(0,9) (S2)=(1,0)

Basia: a co to ma być ?

papanoe: środki zakładam?

Basia: do jakich okręgów ? bo w tych tutaj x²+y² = 6y − 6 x² + y² − 6y +6 = 0 (x−0)²+(y−3)²−9+6=0 (x−0)²+(y−3)² = 3 S₁ = (0,3) r₁ = √3 x²+y² − 2x = 0 (x−1)²+(y−0)²=1 S₂(1,0) r₂ = 1 S₁S₂ = √(1−0)²+(0−3)² = √10

papanoe: srr, błąd.

tomcio: a nie da się tego jakoś wektorami zrobić?

Basia: da się inaczej, i to całkiem prosto P∊OX P(a,0) S₁(0,3) S₂(1,0) no i teraz z tw.Pitagorasa AP² = AS₁²+S₁P² BP² = BS₂²+S₂P² a z warunków zadania AS₁²+S₁P² = BS₂²+S₂P² AS₁=r₁=√3 AS₂=r₂=1 3 + S₁P² = 1 + S₂P² dalej to już łatwizna

tomcio: moge prosić o rusunek?

Basia: rysunek nie chce mi się wczytać; czekaj może się za chwilę uda ( a jeżeli nie to drugi raz nie rysuję); spróbujesz sam

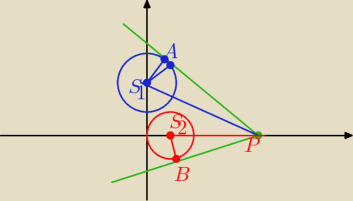
Basia: ∡S_AP i ∡S₂BP są proste będą dwa rozwiązania

Basia: oczywiście S₁AP i S₂BP ma tam być

tomcio: dziękuję bardzo za pomoc