pomocyyy
dorotaaa: w ostrosłupie prawidłowym trójkątnym kąt nachylenia ściany bocznej do płaszczyzny podstawy jest
równy 60 stopni. wysokość ostrosłupa ma 6√3 cm. oblicz objętość i pole powierzchni bocznej
tego ostrosłupa.
26 lis 15:42
dorotaaa:
26 lis 15:53
dorotaaa: w ostrosłupie prawidłowym trójkątnym kąt nachylenia ściany bocznej do płaszczyzny podstawy jest
równy 60 stopni. wysokość ostrosłupa ma 6√3 cm. oblicz objętość i pole powierzchni bocznej
tego ostrosłupa.
26 lis 15:53
dero2005:
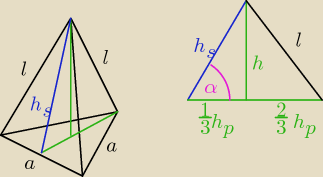
h = 6
√3 cm
| | 2√3 | | 2√3 | |
hs = |
| h = |
| *6√3 = 12 cm
|
| | 3 | | 3 | |
(
13h
p)
2 + h
2 = h
s2
19h
p2 + (6
√3)
2 = 12
2
19h
p2 + 108 = 144 |*9
h
p2 = 1296 − 972 = 324
h
p =
√324 = 18 cm
a =
23√3h
p =
23√3*18 = 12
√3 cm
| | a2√3 | | (12√3)2√3 | |
Pp = |
| = |
| = 108√3 cm2
|
| | 4 | | 4 | |
| | 3 | | 3 | |
Pb = |
| a*hs = |
| *12√3*12 = 216√3 cm2
|
| | 2 | | 2 | |
P
c = P
p + P
b = 108
√3 + 216
√3 = 324
√3 cm
2
V =
13P
p*h =
13*108
√3*6
√3 = 648 cm
3
26 lis 19:49
joebusdriver: @dero2005 jesteś wielki

16 wrz 20:17
h3r0i3: 'a = 23√3hp = 23√3*18 = 12√3 cm' <−−− Skąd to wziąłeś?
16 wrz 21:50
Bogdan:
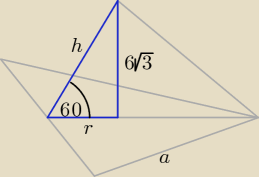
Korzystając z własności trójkąta prostokątnego, którego miara kata ostrego jest równa 60
o
otrzymujemy: r = 6, h = 12
| | 1 | |
r = |
| a√3 /*2√3 ⇒ a = 2r√3 = 12√3 ⇒ a2 = 144*3 |
| | 6 | |
| | 1 | | 1 | |
V = |
| * |
| *144*3*√3*6√3 = ... |
| | 3 | | 4 | |
| | 1 | | 1 | |
Pc = |
| *144*3*√3 + 3* |
| *12√3*12 = ... |
| | 4 | | 2 | |
16 wrz 22:28
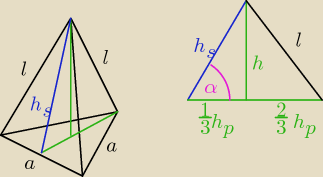 h = 6√3 cm
h = 6√3 cm

 Korzystając z własności trójkąta prostokątnego, którego miara kata ostrego jest równa 60o
otrzymujemy: r = 6, h = 12
Korzystając z własności trójkąta prostokątnego, którego miara kata ostrego jest równa 60o
otrzymujemy: r = 6, h = 12