Bryła wpisana w kulę
ktoś1624: Oblicz objętość ostrosłupa prawidłowego trójkątnego wpisanego w kule o promieniu R, wiedząc, że
krawędź boczna ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem o mierze 60 stopni.
| | 9√3 | |
Prawidłowa odpowiedź to |
| R3 |
| | 32 | |
dero2005:
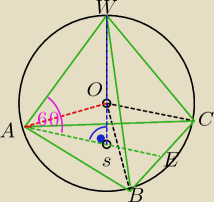
oznaczenia:
|SW| = H → wysokość ostrosłupa
|AE| = h
p → wysokość podstawy (trókąta równobocznego)
|WA| = |WB| = |WC| = l → krawędzie boczne ostrosłupa
|OA| = |OB| = |OC| = |OW| = R → promień kuli
|AB| = |BC| = |CA| = a → krawędź podstawy
rozpatrujemy trójkąt ASW
H = 23√3hp
rozpatrujemy trójkąt ASO
R
2 = (H−R)
2 + (
23h
p)
2
R
2 = H
2 − 2HR + R
2 +
49h
p2 |− R
2
H
2 − 2HR +
49h
p2 = 0 |*9
9H
2 − 18HR + 4h
p2 = 0
9(
23√3h
p)
2 − 18R(
23√3h
p) + 4h
p2 = 0
9(
49*3h
p2) −
363√3h
pR + 4h
p2 = 0
12h
p2 − 12
√3h
pR + 4h
p2 = 0
16h
p2 − 12
√3h
pR = 0 |:4
4h
p2 − 3
√3h
pR = 0
h
p(4h
p − 3
√3R) = 0
h
p = 0 → odrzucamy
4h
p − 3
√3R = 0
4h
p = 3
√3R
hp = 34√3R
z własności trójkąta równobocznego
| | 2 | | 3 | |
a = |
| √3hp = 23√3*34√3R = |
| R
|
| | 3 | | 2 | |
a = 32R
| | 2 | | 2 | | 3 | | 3 | |
H = |
| √3hp = |
| √3* |
| √3R = |
| R
|
| | 3 | | 3 | | 4 | | 2 | |
H = 32R
pole podstawy
| | a2√3 | | (32R)2√3 | | 9 | |
Pp = |
| = |
| = |
| √3R2
|
| | 4 | | 4 | | 16 | |
V =
13P
p*H =
13*
9√3*R216*
3*R2
V = 932√3R3 → objętość ostrosłupa
 oznaczenia:
|SW| = H → wysokość ostrosłupa
|AE| = hp → wysokość podstawy (trókąta równobocznego)
|WA| = |WB| = |WC| = l → krawędzie boczne ostrosłupa
|OA| = |OB| = |OC| = |OW| = R → promień kuli
|AB| = |BC| = |CA| = a → krawędź podstawy
oznaczenia:
|SW| = H → wysokość ostrosłupa
|AE| = hp → wysokość podstawy (trókąta równobocznego)
|WA| = |WB| = |WC| = l → krawędzie boczne ostrosłupa
|OA| = |OB| = |OC| = |OW| = R → promień kuli
|AB| = |BC| = |CA| = a → krawędź podstawy
