Matura rozszerzona OPERON Święty: Chyba nic się nie stanie jak wrzucę kilka zadań z tegorocznej matury rozszerzonej OPERONU. 1) Podaj ujemny pierwiastek równania | |2x−1|−2|=4 2) Prostokąt o bokach a+5, b+5 jest podobny do prostokąta o bokach a,b. Wykaż, że oba prostokąty są kwadratami. 3) W teleturnieju "Jaka to piosenka?" gracz zna 12 na 20 piosenek. Prowadzący wybierze graczowi 4 piosenki. Aby przejść do kolejnego etapu gracz musi podać tytuł co najmniej jednej piosenki. Jakie jest prawdopodobieństwo, że gracz przejdzie do kolejnego etapu? Wynik podaj z dokładnością 0,01.

	1
4) Trojkąt ma boki a,b i jego pole wynosi		ab. Oblicz długość trzeciego boku
	4

	1
5) Dla jakich x		, cosx , sinx tworzą ciąg geometryczny?
	2tgx

6) Dla jakich wartości parametru k, proste y=−x i y=x+k przecinają się w kole (x+1)²+(y+1)²≤10? 7) Wykres paraboli ma wzór f(x)=x²−6x. Punkt C zawiera się w wierzchołku. Punkty A,B znajdują się na paraboli. Podaj współrzedne punktu A lub B dla ktorych trojkat ABC jest rownoboczny. Tak to mniej wiecej wygladało. Oprócz tego bylo zadanie na dowodzenie z logarytmami, z graniastoslupem, parametrem w trojmianie kwadratowym i nierownosc wielomianowa

rumpek: Pisałeś ją?

Vizer: Jak tam rumpek rozszerzenie poszło, okolice setki?

Święty: Pisałem, pisałem. Inaczej bym nie zapamietał Jak wrażenia?

rumpek: No co ty tego 7 (połowę tylko), i wątpliwości z dowodem z logarytmów A mógłbyś obliczyć dla pewności ile wynosi to prawdopodobieństwo ? Bo je zacząłem jako pierwsze

rumpek: Święty ile wyszło ci z tymi ciągami ? i prawdopodobieństwem, w sumie nie było trudne Jedyne wyniki jakie zapamietałem to chyba: To z parametrem m: m∊{1,5} To z wielomianami bodajże: x∊(−1;2)U(3,+∞) To z k to k∊<−4;4> I wynik z prawdopodbieństwem coś kojarze, że z kombinacji zrobiłem

rumpek:

	5
No i naturalnie kojarzę, ze ten pierwiastek z wartości bezwzględnej to x = −
	2

rumpek: Dowód to:

a		a + 5
	=
b		b + 5

a(b + 5) = b(a + 5) ab + 5a = ab + 5b a = b No i rysunki wystarczy tyle na ten geometryczny ?

Święty: Z ciągami:

	π
x=−		+2kπ
	3

	π
x=		+2kπ
	3

Z parametrem, wielomianami, i k mam takie same wyniki

Święty: Dowod tak samo i pierwiastek też tak samo Kiedy beda oficjalne wyniki? Jutro?

rumpek: Prawdopodobieństwo wyszło mi P(A) = 0,985 .. ≈ 0,99

Qlimax: Witam wszystkich mam takie same wyniki jak Wy oprocz tego z k bo tam to zamotałem cos i nie dokończyłem nawet a prawdopodobieństwo wyszlo mi 0.98 ale to chyba zle bo cos dużo mi się wydaje

rumpek: Nom na operonie

Qlimax: a to masz podobnie ja pewnie źle zaokrągliłem

rumpek:

Święty: Ja tez mam 0,99!

rumpek: hmm <myśli> tak myślę nad tym z ciągami, czy mam takie same wyniki. Jak doszedłeś do takiej formy?

rumpek:

	1
cos2x =		* sinx
	2tgx

rumpek:

	1
cos2x =		* sinx
	2sinx   cosx

	cos
cos2x =		* sinx
	2sinx

	cos
cos2x =		/ * sinx
	sinx

...

rumpek: To z trygonometria to każda osoba która zapytam podaje inny wynik

ZKS: A jaki wynik Ci wyszedł rumpek?

rumpek: No własnie tylko jeden Co mnie nie cieszy bo z tego co napisałem: cos²sinx = cosx cos²xsinx − cosx = 0 cos(sinxcosx − 1) = 0 cosx = 0 sinxcosx = 1 / * 2 2sinxcosx = 2 sin2x = 2 (więc teoretycznie nie istnieje bo zbiór wartości to <−1;1>

ZKS: Coś za bardzo za chachmęciłeś ja bym to zrobił tak:

	1
cos2x =		* sinx
	2tgx

	cosx
cos2x =
	2

cosx(2cosx − 1) = 0

Qlimax: a jak Wam wyszło w chyba ostatnim zadaniu, gdzie trzeba było obliczyć 3. bok trójkąta?

Vizer: Jeśli potrzebujecie potwierdzenia to wg mnie prawdopodobieństwo wychodzi 0.99

rumpek: Już widze gdzie mam błąd było 2sinx, a nie sin^x Ale chociaz jeden wynik poprawny No cóż będzie koło hmm<myśli> 50 − 3 − 3 − 1 = 50 − 7 = 43 pkt blehh mam nadzieje, że nie zrobię błędu na głównej

rumpek: 3 boku trójkąta, to z twierdzenia cosinusów. nie pamietam dokładnie wynik, a nie chce mi sie znowu liczyć Kto zrobił ten dowód z logarytmem? Ja tam zmieniłem podstawy do log₁₀ itp.

Vizer: 86% nie byłby złym wynikiem i jak na maturę próbną, z tego co sobie liczysz, poszło Ci na prawdę dobrze

ZKS: To i tak nieźle jeżeli 43 pkt gratuluję. A pamiętasz jak wyglądało to na dowodzenie z logarytmami chętnie bym na nie spojrzał.

ICSP: To była maturka podstawowa czy rozszerzona?

Vizer: A co ci nie widać ICSP, że rozszerzona?

rumpek: Hmmm zaraz coś skrobnę

ICSP: Jak spojrzałem na zad2 to zwątpiłem Może teraz to wszystko mi się wydaje jakieś łatwiejsze

rumpek: log²(aπ) + log²(π + a) ≥ tutaj coś zaraz przemyśle i napisze

rumpek: log²(πa) + log²(π+a) ≥ tutaj jeden element − log_ππ

rumpek: I tego elementu nie miętam wiem tylko, że zastosowałem wzór:

1
	= logba
logab

rumpek: Oczywiście warunek a>0 i wykazać, że jest prawdziwa

rumpek:

2
	(to chyba ten brakujący element)
logπ + a10

chociaz głowy nie dam

ZKS: I niestety nie przypomnisz sobie tego brakującego elementu?

rumpek: Czyli sumując: Wykaż, że prawdziwa jest nierówność wiedząc, że a jest dodatnie.

	2
log2(πa) + log2(π+a) ≥		− logππ
	logπ + a10

rumpek: tam może niepoprawnie być tylko podstawa logarytmu pod ułamkiem

rumpek: ale raczej poprawnie no i zamieniłem tam:

	1
log2(πa) + log2(π+a) ≥ 2 *		− 1
	logπ + a10

1
	= 2log(π + a)
logπ + a10

ZKS: Jeżeli tak zamieniłeś to wszystko w porządku teraz to już z górki.

rumpek: Możesz dokończyć ? Bo nad tym dowodem myślałem najdłużej

Bartek0807: bardzo mnie interesuje rozwiazanie do 6−tego zadania bodajże. Było to zadanie o graniastosłupie prawidłowym czworokątnym gdzie krawędź podstawy wynosiła 2a a kąt między przekątną podstawy a przekatną sciany bocznej wynosił α. Trzeba bylo wyznaczyć objetość. Chyba tak to było I jeszcze ostatnie zadanko gdzie wyznaczyc trzeba bylo bok C Nie pamiętam czy tak to pierwsze zadanie brzmiało wiec proszę wziać poprawkę na to

ZKS: (log π + log a)² + log²(π + a) − 2log(π + a) + 1 ≥ 0 (log π + log a)² + (log (π + a) − 1)² ≥ 0 Jeżeli się nie pomyliłem to chyba tak.

rumpek: Cwane niestety tak nie zrobiłem. Myślisz, że uznają to jak ktoś udowodnił, że prawa strona będzie zawsze większa lub równa lewej? mianowicie:

	π + a
log2(πa) + log2(π + a) ≥ log(		)2
	10

I komentarz, że podstawiając dowolną liczbę za a większą od zera otrzymamy nierówność prawdziwą?

rumpek: Nie miałem pomysłu na to jak dokończyć w sumie rok temu maturka rozszerzona z operonu była łatwiejsza.

ZKS: Wiesz ile miałem procent z rozszerzonej matury próbnej z operonu w tamtym roku? Heh wstyd aż mówić tak dobrze ją napisałem. Więc jeszcze zobaczysz że wszystko będzie szło bez problemu jeżeli będziesz rozwiązywał dużo zadań. A z Twoim udowodnieniem to ciężko mi powiedzieć czy Ci zaliczą na 100% to zadanie ale minimum 2 pkt z tego na pewno dostaniesz.

Lola: W tym zadaniu z wartością bezwzględną nie powinno być dwóch pierwiastków ujemnych? −0,5 i −3,5?

Lola: nie −3,5 tylko −2,5 mój błąd

ZKS: Taka mała wskazówka jeżeli masz jakąś nierówność do udowodnienia to zawsze sprawdź najpierw czy to się nie złoży do wzoru skróconego mnożenia.

rumpek: ZKS nawet podstawiłem za a 1 itp. Także sie zastanawiam, teoretycznie prawdziwe.

rumpek: właśnie szukałem ale nie znalazłem i po 1,5h oddałem maturkę moglem jeszcze pogłówkować

ZKS:

	1
Podstaw i zobacz czy −		spełnia to równanie.
	2

ZKS: Jeżeli dałeś jakiś komentarz słowny do tego udowodnienia to może Ci zaliczą.

rumpek: No pewnie I to jaki komentarz drugi Mickiewicz ze mnie

Bartek0807: Wieszczu: indukcja i po problemie

ZKS: To tak jak ja na majowej maturze dłuży dałem komentarz swojego udowodnienia niż napisałem rozprawkę z polskiego.

rumpek: Indukcji to ja jeszcze sobie nie przerabiałem

Bartek0807: pomaga i to nawet nie musisz za duzo główkować oszczędność czasu polecam

jarke: w tym zadaniu z graniastosłupem, trzeba było napisać, że cosα= połowa przekątnej podstawy przez przekątną graniastosłupa i później podstawić do trójkąta w którym jest bok podstawy, wysokość graniastosłupa i przekątna graniastosłupa i wyliczyć H i napisać wzór na objętość, dobrze główkuję? a i w tym ciągu, będą ujemne punkty jeśli nie napisało się założeń cosx≠0 sinx≠0 i 2tgx≠0 ?

Vizer: Założenia rzecz święta.

Nienor: Na pewno. Bo z dziedziny odpada ci rozwiązanie. Teraz żałuję, że nie pisałam dzisiaj matematyki, bo fizyka to była porażka.

jarke: Treść zadania z graniastosłupem: W graniastosłupie prawidłowym czworokątnym długość grawędzi podstawy jest równa 2a. Miara kąta między przekątną podstawy, a przekątną ściany bocznej wychodzącą z tego samego kąta wynosi α. Oblicz objętość graniastosłupa.

nieokiełznany: mi wyszło coś takiego

	2 + cos2α
V = 8a2√
	1 + cos2α

jarke: to mi coś innego, już bo nie pamiętam co mi wyszło

Chiara: mi wyszło 4a²2a√2*tgα

Chiara: a zrobił ktoś to zad z tą parabolą i trójkątem równobocznym?

jarke: mi wyszedł taki wynik:

	(√2−2cosα)
V=a[4a*		]
	cosα

jarke: ja niestety nie, narysowałem parabolę, wyznaczyłem współrzędne punktu c i na tym się skończyło u mnie...

	1
a zrobił ktoś ostatnie zadanie to o trójkącie o polu		ab mają długości boków a i b,
	4

obliczyć długość trzeciego boku?

Vizer: Pewnie w tym zadaniu trzeba będzie wykorzystać fakt, że tg60=a.

Vizer: Pisze o zadaniu z parabolą i trójkątem równobocznym.

Chiara: ja tak samo jak jarke, ciekawe czy za to urwie sie chociaż jakiś punkt

Bartek0807: nie wiem czy wyszło mi dobrze ale zrobiłem to intuicyjnie. Narysowalem parabole i zauważyłem że im dalej od środka paraboli tym bardziej ramiona nie są równe podstawie. A przecież o to chodzi by wszystkie boki były rowne. Podstawiłem równanie x² − 6x= ^x√3₂ wyliczyłem wyszło mi cos koło 3 x co pasowało do rysunku. ^x√3₂ to ^a√3₂ − wysokość trójkąta równobocznego Czy zrobiłem dobrze?

jarke: Chaira nie jestem sam z takim wynikiem, tak jest : D może policzy to ktoś jeszcze z obecnych? albo Jakub, jak znajdzie chwilkę ; )

Patryk: czy jedna z prostych tworzących trójkąt równoboczny wyglądała tak y=√3x−14,18 ?

ZKS: d² = (2a)² + (2a)² ⇒ d = 2√2a

	h
tgα =
	1   d 2

√2atgα = h V = 4a² * √2atgα = 4√2a³tgα Chyba tak ale geometria nie jest moją mocną stroną.

TOmek: "Wykres paraboli ma wzór f(x)=x2−6x. Punkt C zawiera się w wierzchołku. Punkty A,B znajdują się na paraboli. Podaj współrzedne punktu A lub B dla ktorych trojkat ABC jest rownoboczny." Podobne zadanie robiłem wczoraj

jarke: ZKS dlaczego bierzesz wysokość tego trójkąta do wzoru na objętość, a nie wysokość graniastosłupa?

ZKS: Już widzę gdzie mam błąd d₁ − przekątna ściany bocznej

	1   d 2
cosα =
	d1

	d
d1 =
	2cosα

(2a)² + h² = d₁²

	√2a
h2 =		− 4a2
	cosα

	√2a
h = √		− 4a2
	cosα

	√2a
V = 4a2 * √		− 4a2
	cosα

√2a
	− 4a2 jest pod całym pierwiastkiem
cosα

jarke: bo mi tak coś pasowało, teraz zgadza się, czyli mam dobrze ; ) bo −4a² sprowadziłem wspólnego mianownika, czyli cosα i wyciągnąłem przed nawias co się dało

ZKS: Jej i znowu źle.

	2a2
h2 =		− 4a2
	cos2α

jarke: tak, zgadza się, nie zwróciłem uwagi na błąd

ZKS: Ostatecznie:

	√−cos2α		√−cos2α
V = 4a2 * √2a		= 4√2a3
	cosα		cosα

Patryk: 25 lis 17:34 ?

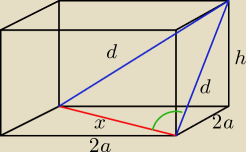
słabo: Ja to robiłem tak ael jakieś głupoty chyba powychodziły : I. x = 2a√2 II. Z twierdzenia cosinusów: d² = x² + d² − 2*x*d*cosα x² − 2*x*d*cosα = 0 x² = 2*x*d*cosα

	x2
d =
	2*x*cosα

	x		2a√2		a√2
d =		⇒		⇒
	2cosα		2cosα		cosα

III. Z Pitagorasa: h² + (2a)² = d²

	a√2
h2 + 4a2 = (		)2
	cosα

	2a2
h2 + 4a2 =
	(cosα)2

	2a2		4a2*(cosα)2
h2 =		−
	(cosα)2		(cosα)2

	2a2 − 4a2*(cosα)2
h2 =
	(cosα)2

	2a2*(1 − 2*(cosα)2)
h2 =
	(cosα)2

	√2a*√1 − 2*(cosα)2
h =
	cosα

	√2a*√1 − 2*(cosα)2
V = (2a)2 *
	cosα

Patryk: to do 7

Święty: I jak oceniacie poziom tej matury? W porównaniu z zeszłoroczną maturą próbną trudniejsza.

Asia: Kurcze zdecydowanie trudniejsza. Robiłam testy z operonu z ostatnich 3−4 lat i nie miałam problemów a dzisiaj klapa. Może ponad 40% będę miała ale kiepsko. Ale za to może jak CKE zobaczy wyniki tej matury i dostrzeże, że słabo poszła to da łatwiejsza w maju

c: ββδπΔ

Godzio: Nie znowu aż taka trudna