Udowodnienia ICSP: Dwa na które nie mam pomysłu Udowodnij że jeżeli środek okręgu wpisanego w czworokąt jest jednocześnie punktem przecięcia przekątnych to czworokąt ten jest rombem. i drugie: Na czworokącie ABCD można opisać okrąg. Niech P,Q,R i S będą rzutami prostokątnymi punktu przecięcia przekątnych czworokąta na proste zawierające kolejne boki. Udowodnij że w czworokąt PQRS można wpisać okrąg.

ICSP: drugie zrobiłem Wiem żałosne było Zostało jeszcze pierwsze xD

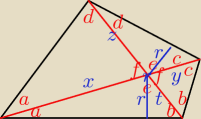
Basia: przekątne są dwusiecznymi (wynika z treści zadania) stąd oznaczenia na rysunku liczymy kąty: e= 180−(a+b) f = 180 −e = a+b c = 180−f−b = 180−a−2b d = 180−e−c = 180 − 180 + a+b −180+a+2b = 2a+3b−180 a+d+f = 180 a+2a+3b−180+a+b = 180 4a+4b = 360 a+b = 90 czyli przekątne przecinają się pod kątem prostym ponadto 2b = 180−2a c = 180 −a − 180+2a = a 2c = 2a d = 2(90−b)+3b − 180 = b 2b = 2d czyli przeciwległe kąty są równe no to mamy równoległobok, którego przekątne przecinają się pod kątem prostym ponadto sina = ^r_x sinc − sina = ^r_y czyli x=y analogicznie z=t no to mamy równoległobok, którego przekątne przecinają się pod kątem prostym i w połowie no to już nie ma mocnych mamy romb

Basia: tam oczywiście ma być sinc = sina (a nie −)

Basia: ICSP może być ?

ICSP: oczywiście że może być Dziękuję Basiu