Zadanie maturalne -OPERON Ky$: W trójkącie prostokątnym jedna z przyprostokątnych ma długośc a. Kąt ostry przy tym boku ma miarę α. Wykaż, że sinα + cosα > 1 Jest to zadanie maturalne, z próbnej matury z operonem ze wczoraj. I moje pytanie jest następujące, czy moja metoda którą zaraz zaprezentuję gwarantuje mi maximum punktów tj. 2, czy też nie ? sin² + cos² = 1 Korzystam z własności jedynki trygonometrycznej. potęguję obustronnie wyrażenie: sinα + cosα > 1 /()² (sinα + cosα)² > 1 sin²α +2sinαcosα+ cos²α > 1 sin²α + cos²α +2sinαcosα > 1 1 + 2sinαcosα > 1 2sinαcosα > 1−1 2sinαcosα > 0 A jeżeli nasze wyrażenie jest większe od zera to mamy udowodnioną nierównosc : sinα + cosα > 1 Co Wy na to? Pytam dlatego, że w wynikach matur jest podane inne rozwiązanie, a mianowicie z własnosci trojkata, że suma przyprostokątnych jest większa od przecwprostokatnej zamieniając lewą strone nierównosci na: sin^α + cosα = ^b_c+^a_c=^a+b_c co w efekcie daje nam rownanie: ^a+b_c > 1 czyli sinα + cosα > 1

Basia: pod warunkiem, że napisałeś wyraźnie, że dla α∊(0,90) sinα, cosα>0 z czego wynika, że sinα+cosα>0 i sinα*cosα>0

Jack: to założenie wynika z treści zadania (Δ prostokątny), nie znam standardów oceniania ale myślę że dużo by nie stracił.

Ky$: Założeń takowych nie pisałem, całosc mojego zadania jest u góry

Jack: skoro w kluczu nie pisali, że a,b,c>0, to Ty też możesz być usprawiedliwiony gdy nie pisałeś, że sinα, cosα>0 Choć podnosząc obie strony do kwadratu, powinieneś zwrócić na to uwagę że sinα+cosα>0 ...

Basia: w rozwiązaniu podanym w kluczu niczego nie podnoszą do kwadratu i to jest ta drobna różnica, bo jednak równania a=b i a²=b² zasadniczo nie są równoważne (tz. są równoważne tylko w określonych przypadkach, z których jeden tu zachodzi: a,b > 0; drugi to a,b<0)

Ky$: No niby powinienem uwzględnic ze α∊(0,90), no ale jak już sam Jack zauważył, ów założenie wynika z treści zadania, czyli nie jako nikt sie nie uprze, że z mojego zadania może wynikac trójkąt o ujemnych scianach, bo cos takiego nie istnieje... Czyli koniec końców, jak egzaminatorzy patrzą na takie, że się tak wyrażę niedopatrzenie.. ?

rumpek: Sprawdzają to twoi nauczyciele A nie egzaminatorzy − na razie Główną rzecz jasna egzaminatorzy.

Ky$: to, to i ja wiem, ale można ich potraktowac jako egzaminatorów, bo sugerowac beda się kluczem, a nie swoim wydzimisiem, czy też sympatią do danego ucznia...

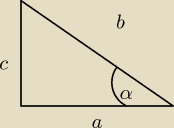
erni: ja to zadanie zrobiłem w 3 linijkach i poglądowym rysunku sinα+cosα>1

b		a
	+		>1
c		c

a+b
	>1/*c
c

a+b>c i to zawsze jest większe od 1, inaczej nie dałoby się stworzyć trójkąta

erni: ups, za szybko i oznaczenia na rysunku są pomylone, ale schemat jest ok.