dlaczego tutaj trzeba rozważyć przypadki? elpolaco: x+2<√x+14 ?

ICSP: a trzeba?

Jack: wszystko zależy od metody rozwiązania zadania...

ICSP: ja bym to sprowadził do równania kwadratowego. Zrobił podstawienie t = √x+14 t≥0 i po problemie.

elpolaco: zrobiłem tak x² + 4x + 4 < x+14 x²+3x−10<0 x=−5 , x=2 rozwiązanie x∊(−5;2) jednak w odpowiedziach jest inaczej....

Vizer: Nie możesz podnieść do kwadratu nie wiedząc jaką wartość masz po lewej stronie.

elpolaco: a jest na to jakies twierdzenie? dlaczego nie moge?

Vizer: Jeśli nie masz pewności jaki znak (czy + czy −) masz po lewej stronie nie możesz podnieść do kwadratu, bo nawet nie wiesz, w którą stronę zwrócić nierówność.

elpolaco: ale po podniesieniu do kwadratu liczba zawsze będzie dodatnia....nie rozuemiem

sushi_ gg6397228: −3 < 2 podnies do kwadratu 9< 4 nierownosc FAŁSZYWA

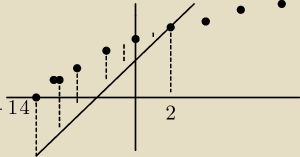
AS: A może tak Zał 1. x >= −2 wtedy (x + 2)² < x + 14 => x² + 3*x − 10 < 0 => x ∊ <−5,2) Zał. 2. x < −2 , wtedy lewa strona jest ujemna dla każdego x z zał. czyli prawdą jest,że P{x + 14} >= 0 => x + 14 >= 0 => x >= −14 Rozwiązaniem: x ∊ <−14,2) Potwierdza do wykres

ICSP: ależ po co sie bawić w załozenia? x+2 < √x+14 D : x ≥−14 i lecimy: x +14 −√x+14 − 12 < 0 t = √x+14 t ≥ 0 − z przyczyn oczywistych t² − t − 12 <0 liczymy deltę i t t₁ = 4 t₂ < 0 czyli sprzeczne t₁ = 4 ⇔ 4 = √x+14 ⇔ x = 2 czyli odp. x ∊ <−14;2)