. Iza: potrzebuję pomocy, jak rozwiązać takie zadanie: znaleźć zbiór punktów z których elipsę o równianiu ^x2₉ + ^y2₁₆=1 widać pod kątem prostym.

Iza: umie ktoś wytłumaczyć mi to zadanie ?

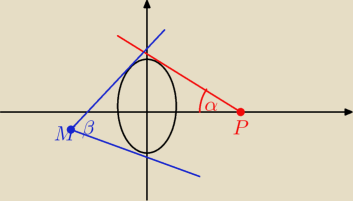
Basia: z punktu P patrzę na elipsę pod kątem α chodzi chyba o styczne do elipsy prostopadłe do osi OX a takie są dwie x=3 i x=−3 ale nie jestem pewna bo nie bardzo rozumiem sformułowanie "widać pod kątem prostym" próbuję na coś spojrzeć pod kątem prostym i wydaje mi się, że to jest fizycznie niemożliwe −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− a może chodzi o tę sytuację "niebieską" zbiór tych punktów, dla których te dwie styczne są do siebie prostopadłe

Iza: w takim razie jak wyznaczyć te dwie prostopadłe do siebie styczne ?

Basia: 16x² + 9y² =144

	√144−16x2		√16(9−x2)		4√9−x2
y = ±		= ±		= ±
	3		3		3

współczynnik kierunkowy stycznej = y' i może to być

	4		1		4x
a= ±		*		*(−2x) = ±
	3		2√9−x2		√9−x2

a₁*a₂ = −1

	16x2
±		= −1
	9−x2

czyli mamy możliwości 16x² = −(9−x²) lub −16x² = −(9−x²) 15x² = −9 niemożliwe lub −15x² = −9 x² = ⁹₁₅

	3√15		√15
x =		=
	15		5

lub

	√15
x = −
	5

stąd

	4√9−1525		4√9*25−15		4√15(15−1)
y = ±		= ±		= ±		=
	3		3*5		15

	4√15*14
±
	15

byłyby więc 4 takie punkty:

	√15		4√210
A (		;		)
	5		15

	√15		4√210
B (		; −		)
	5		15

	√15		4√210
C (−		;		)
	5		15

	√15		4√210
D (−		; −		)
	5		15

ale naprawdę nie wiem czy o to chodzi

Basia: kompletną bzdurę tam wyżej napisałam; wszystko poknociłam to trzeba zupełnie inaczej

Basia: mamy mieć dwie styczne prostopadłe są dwie możliwości 1. styczne są równoległe do osi wtedy jedna ma równanie y=y0, druga x=x0 można to liczyć formalnie, ale chyba nie ma sensu gołym okiem widać, że są to proste: y = 4 y= −4 x = 3 x = −3 czyli mamy tu cztery punkty spełniające warunki zadania: A(3,4) B(−3,4) C(−3,−4) D(3,−4) 2. styczne nie są równoległe do osi wtedy jedna musi mieć równanie y = ax+b1 druga y = −u{1}[a}x+b2 obie przechodzą przez jakiś punkt M(x0,y0) stąd y0 = ax0+b1 b1 = y0−ax0 k: y=ax+(y0−ax0) y0 = −1ax0 + b2 b2 = y0+1ax0 = ay0+x0a l: y = −1}[a}x + u{ay0+x0a l: y = −ax+ay0+x0a zatem każdy z układów równań (1) y=ax+(y0−ax0) 16x2+9y2=144 (2) y = −ax+ay0+x0a 16x2+9y2=144 musi mieć jedno i tylko jedno rozwiązanie podstawiamy za y, dostajemy dwa równania kwadratowe z niewiadomą x i w każdym badamy warunek Δ=0 dostaniemy w ten sposób jakieś dwa równania z a,x0,y0 rozwiązujemy układ tych równań co da nam jakąś zależność między y0 i x0 (lub konkretne wartości x0 i y0, ale wątpię) po opuszczeniu wskaźników ta zależność opisuje krzywą którą utworzą punkty spełniające warunki zadania rachunki to będą żmudne, ale wykonalne