Określ wzajemne położenie prostej l i okręgu o, jeśli; Krzychu: o: x²+y²+8x−2y+13=0; l: y=x

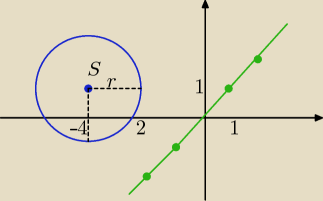
Eta: Jeżeli zadanie jest zamknięte.. wystarczy narysować okrąg i prostą w ukł. współrzędnych o:(x+4)²+(y−1)²=4 S(−4,1) r=2

rumpek: Ostatnie zadanie na dzisiaj: x² + y² + 8x − 2y + 13 = 0 (x² + 8x + 16) − 16 + (y² − 2y + 1) − 1 + 13 = 0 (x + 4)² + (y − 1)² = 4 S = (−4, 1) r = 2 Liczę odległość prostej y = x od środka okręgu: −x + y = 0

	|(−1) * (−4) + 1 * 1 + 0|		|4 + 1|
d =		=		=
	√(−1)2 + 12		√2

	5		√2		5√2
		*		=
	√2		√2		2

d > r także nie są styczne (0 pkt wspólnych). Jakby gdzieś się pomylił w obliczeniach to sobie popraw.

Eta:

rumpek:

Krzychu: Bardzo dziękuje

patt: x² +y² = 1 L: y=x

patt: wzajemne połozenie prostej i okregu

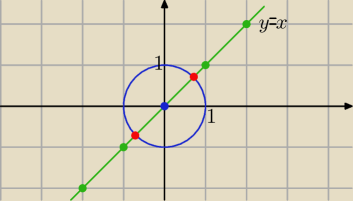
Eta: prosta jest sieczną tego okręgu −−−−− ma z nim 2 punkty wspólne

patt: a śa do tego jakies obliczenia ?

Janek191: Eto − proszę zajrzeć na forum/188832.html

Mateusz: Tak robisz analogiczne obliczenia jak rumpek

patt: Dziekuje bardzo . a jezeli x ²+y² −1=0 −x+y=0 i obliczyc układem równan?

Mateusz: Znaczy jesli masz wyznaczyć punkty wspolne prostej o tego okręgu to wtedy układ równan rozwiązujesz