Prosta o wspólczynniku kierunkowym rownym 2, przechodzą przez punkt P(-1;3) ma r
Mateusz: 1Prosta o wspólczynniku kierunkowym rownym 2, przechodzą przez punkt P(−1;3) ma rownanie:
A. y=2x+1
B. y=2x+3
C. y=2x+5
D. y=−2+3
Prosze o udzielenie rozwiazania i sposobu rozwiązywania. z gory dziekuje
Dane są okregi opisane rownaniami : (x+2)
2+y
2=4 i x
2+(y−2)
2=9. Odległość miedzy środkami
tych okręgów jest równa:
A. 2
√5
B.
√5
C.
√6
D.4
Prosze o udzielenie rozwiazania i sposobu rozwiązywania. z gory dziekuje
22 lis 22:53
aa: 1 c
22 lis 22:54
Mateusz: Dane są okregi opisane rownaniami : (x+2)2+y2=4 i x2+(y−2)2=9. Odległość miedzy środkami tych
okręgów jest równa: A. 2√2 B. √13 C. 4 D.9 Prosze o udzielenie rozwiazania i sposobu
rozwiązywania. z gory dziekuje
Porpawione odpowiedzi tutaj
22 lis 22:56
aa: S=(a, b) (x−a)2+(y−b)2=r2
wiec 2√2
22 lis 22:58
aa: 1. współczynnik kierunkowy to to co stoi przy x więc y=2x+b i przechodzi przez punkt więc
P(−1, 3)∊y=2x+b ⇒3=2*(−1)+b
3+2=b więc y=2x+5
22 lis 23:00
Mateusz: Dzieki za wzór ale jak to rozwiązales bo niepotrafie se poradzić
22 lis 23:01
Mateusz: chodzi mi o 2 zadanie czy bys mogł wytlumaczyć
22 lis 23:02
aa:
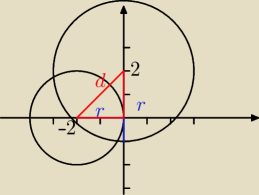
(x+2)
2+y
2=4
S=(−2, 0)
i x
2+(y−2)
2=9
S=(0, 2)
2
2+2
2=d
2
d
2=8
d=2
√2
22 lis 23:07
dero2005:
(x+2)2 + y2 = 4
S1(−2 , 0)
x2 + (y−2)2 = 9
S2(0 , 2)
wzór na odległość dwóch punktów
d = √(x2−x1)2 + (y2−y1)2
d = √0+2)2 + (2−0)2 = √22+22 = √8 = 2√2
23 lis 08:14