Nie ogarniam.... pomocy Masza: Wyznacz krawedz podstawy ostroslupa prawidlowego trojkatnego o objetosci 2√26 wiedzac ze krawedz boczna jest 3 razy dluzsza od krawedzi podstawy

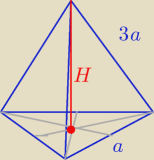
rumpek: Wpierw rysuneczek

rumpek: 1^o Obliczam małą wysokość (h_m)

	a
(hm)2 + (		)2 = (3a)2
	2

	a2
hm2 +		= 9a2
	4

	a2
hm2 = 9a2 −
	4

	36a2		a2
hm2 =		−
	4		4

	35a2
hm2 =
	4

	√35a
hm =
	2

2^o Obliczam dużą wysokość (H)

	a		√35a
H2 + (		)2 = (		)2
	3		2

	a2		35a2
H2 +		=
	9		4

	35a2		a2
H2 =		−
	4		9

	315a2		4a2
H2 =		−
	36		36

	311a2
H2 =
	36

	√311a
H =
	6

I teraz trzeba sprawdzić czy nie ma błędu a potem podstawić pod równanie i otrzymasz a.

rumpek: Tak rozwiązanie ma "buga" zaraz "zreperuje"

rumpek: Po namyśle wcale nie trzeba liczyć h_m, ponieważ wystarczy: 1) Z twierdzenia Pitagorasa − bierzesz 2/3 wysokości podstawy, wysokość H ostrosłupa, oraz krawędź boczną:

2		a√3		2a√3		a√3
	*		=		=
3		2		6		3

	a√3
H2 + (		)2 = (3a)2
	3

	3a2
H2 +		= 9a2
	9

	3a2
H2 = 9a2 −
	9

	a2
H2 = 9a2 −
	3

	27a2 − a2
H2 =
	3

	26a2
H2 =
	3

	a√26		√3		a√78
H =		*		=
	√3		√3		3

Zaraz sprawdze czy tu nie ma błedu

rumpek: wracając do tamtego sposobu teoretycznie poprawny ale trzeb wprowadzić poprawkę w 2^o

	a		1		a√3
Tam gdzie dałem		powinno być:		*		..
	3		3		2

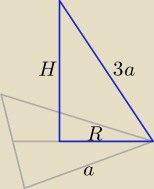Bogdan: Po prostu:

	1		3		78		1
R =		a√3, H2 = 9a2 −		a2 =		a2, H =		a√78
	3		9		9		3

	1		1
2√26 =		*		a2√3 * H / * 4√3 ⇒ 8√78 = a2H
	3		4

	1		3
8√78 = a2 *		a√78 / *		⇒ a3 = 8*3 ⇒ a = 23√3
	3		√78

rumpek: Ja po prostu trenuje obliczenia przed maturą próbną rozszerzoną, którą będę pisał w piątek