Dany jest czworościan ABCD, w którym nowy234: ∀ADB=∀BDC=∀CDA=90 stopni Oblicz objętość czworościanu, jeżeli DA=48 DB=49 DC=50

Basia: z tego zapisu wynika, że ściany boczne to trójkąty prostokątne no to policz AB, AC i BC z tw. Pitagorasa i zobaczymy jakim trójkątem jest podstawa

nowy234: wiem też tak liczyłem i wyszło że to normalny trójkąt

nowy234: nie wiem potem co dalej

Basia: to napisz jakie są te długości boków podstawy; może jak je zobaczę coś wymyślę

nowy234: AB=√4705 AC=√4804 BC=√4901 jeżeli jeszcze jestes

Basia: rzeczywiście nic to nie daje, no pole podstawy można policzyć np. z wzoru Herona ale nie wiem skąd wziąć wysokość nic więcej w tym zadaniu nie było powiedziane ? jeżeli nie to zajrzyj jutro; może coś komuś przyjdzie do głowy (ja też będę myśleć)

nowy234: no niestety nie a ogólnie dzięki za zajęcie swojego cennego czasu

Basia: ciekawe to zadanie; możesz napisać skąd go masz ?

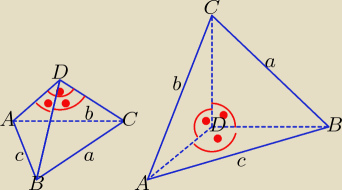
Bogdan: A może postawić czworościan na jednej z ścian, która jest trójkątem prostokątnym. Podaję na rysunku przykład. Teraz wysokością jest CD.

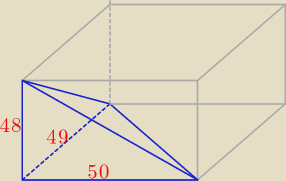
Bogdan: To tak, jakbyśmy wycięli czworościan z prostopadłościanu.

Basia: Oczywiście Bogdanie, właśnie weszłam, żeby to samo napisać; jakieś zaćmienie mnie wczoraj dopadło albo dałam się literkom zasugerować ; przecież każdy czworościan mogę sobie "postawić" na dowolnej ścianie i uznać ją za podstawę; Pozdrawiam

Bogdan:

nowy234: dzieki nie pomyślałbym o tym że to tak może byc

Bogdan: Powtórzę myśl już dzisiaj na forum wypowiedzianą. Umiejętność rozwiązywania zagadnień (nie tylko zadań szkolnych), to w bardzo dużym stopniu sztuka kojarzenia.