Przedziały wklęsłości i wypukłości Gosia: Wyznaczyć przedziały wklęsłości i wypukłości funkcji: a) p(x)=(x−1)e ^1_x−1

	1
b) q(x)=
	√x2−1

wiem jak należy postępować, tzn, obliczyć pochodną pierwszą i drugą a później >0 <0 ale źle coś robię, bo dziwne rzeczy mi wychodzą, więc proszę o pomoc: a) p'(x)=(x−1)'*e ^1_x−1 +(x−1)*(e ^1_x−1 )'=e ^1_x−1 +(x−1)*e ^1_x−1 *

	−1		e 1x−1		1
		= e 1x−1 −		=e 1x−1 (1−		)
	(x−1)2		x−1		x−1

a druga:

	e 1x−1		−1
p''(x)=(e 1x−1 )'− (		)'=e 1x−1 *		−
	x−1		(x−1)2

	(e1x−1 )'(x−1)−(e 1x−1 )(x−1)'		e 1x−1
		=
	(x−1)2		(x−1)3

	1		−x
b)q'(x)= −		(x2−1) −32 *2x=
	2		√(x2−1)3

a druga:

	(−x)' √(x2−1)3+x (√(x2−1)3)'
q''(x)=		=−(x2−1) √x2−1+ U{x2(x2−1)}{
	(x2−1)3

√x²−1 }

Gosia: http://www.matematyka.pl/272582.htm#p4820671

sushi_ gg6397228: to za krotko siedzisz

Gosia: pomoże ktoś na serio...nie wychodzi mi

sushi_ gg6397228: dziedzina (−∞, −1) u(1,+∞)

	−1 * (..)3/2 + x* 1,5* (...)1/2 * 2x
q '' =		=
	(x2−1)3

−1 * (...)3/2 + 3x2(...)1/2 * 2x
	=
(x2−1)3

−1 * (...)* (...)1/2 + 3x2(...)1/2
	=
(x2−1)3

−1 * (...)* √(...) + 3x2 √(...)
	=
(x2−1)3

	√(....) (−x2+1+3x2)
=		=...
	(x2−1)3

	√(x2−1)* (2x2+1)
=		=...
	(x2−1)3

widac, ze dla podanej dziedziny kazdy nawias + wyrazenie pod pierwiastkiem sa DODATNIE zatem q ' ' >0 dla kazdego x z dziedziny

Basia: ad.a błąd przy liczeniu pierwszej pochodnej

	1		1		1
(11−x)' = −		*(1−x)' = −		*(−1) =
	(1−x)2		(1−x)2		(1−x)2

dalej musisz poprawić i wtedy powinno wyjść co trzeba ad.b

	1		1		−x
q'(x) = −		*		*2x =
	x2−1		2√x2−1		(x2−1)3/2

zgadza się błąd jest tutaj:

	f'*g − f*g'
(fg)' =
	g2

sushi_ gg6397228: przeciez tam jest (x−1) a nie (1−x)

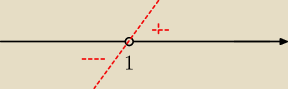
sushi_ gg6397228: wiec p'' (x) >0 dla x>1 f. rosnaca p '' (x)<0 dla x<1 f. malejaca

Basia: no to widocznie źle przeczytałam

Gosia: sushi dziękuję, a a) mam dobrze?

sushi_ gg6397228: jest bład w odpowiedziach tutaj masz wykres http://www.wolframalpha.com/input/?i=%28x-1%29*e^{1%2F%28x-1%29}

sushi_ gg6397228: raczej mialo byc p '' (x) > 0 −−−> wypukla p '' (x) < 0 −−> wklesla

Gosia: dziękuję