równianie prostych tomek: Napisz równania prostych stycznych do okręgu o i prostopadłych do prostej k o: (x−5)²+y²=9 k: y=−x powinno wyjść y=x−5+ 3√2 lub y=x−5−3√2

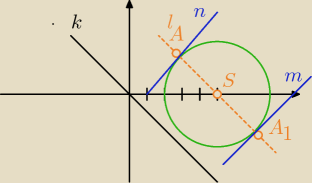
dero2005: prosta l: ma współczynnik kierunkowy (−1) (jest równoległa do prostej k: y = −x) i przechodzi przez punkt S(5, 0) y = −1(x − 5) + 0 = −x + 5 SA^→ [a,b] = [x_A−5 ,y_A−0] |SA|^→ = √a² + b² = √(x_A−5)² + (y_A)² = 3 → długość wektora SA jednocześnie punkt A należy do prostej l: czyli y = −x + 5 dla lepszego obrazu opuszczamy indeks A √(x−5)² + (−x+5)² = 3 |² (x−5)² + (−x+5)² = 9 x² − 10x + 25 + x² − 10x + 25 − 9 = 0 2x² − 20x + 41 = 0 Δ = 400 − 8*41 = 72 √Δ = 6√2

	10−3√2		10+3√2
x1 =		x2 =
	2		2

y = −x + 5

	3√2		−3√2
y1 =		y2 =
	2		2

Punkt A ma współrzędne (x₁, y₁) prosta n jest prostopadła do prostej k: (ma współczynnik kierunkowy 1) i przechodzi przez punkt A y_n = a_n(x − x₁) + y₁

	10−3√2		3√2
yn = 1(x −		) +		= x + 3√2 − 5
	2		2

prosta m jest prostopadła do prostek=j k: i przechodzi przez punkt A₁ punkt A₁ ma współrzedne (x₂, y₂) y_m = a_m(x − x₂) + y₂

	10+3√2		−3√2
ym = 1(x −		) +		= x − 5 − 3√2
	2		2

Janek: Sondaż na temat filmu: nie podobal się 6, średni 7, niezly 8 fajny 3. Przyporządkuj wynikom sondażu oceny 1,2,3,4. Oblicz średnią arytmetyczną, medianę, odchylenie standardowe ocen.