kulki 2: nie wiem jak i jakich wzorów zastosować a mam takie zadanie w urnie jest 7 kul białych i 5 czarnych wylosowano dwa razy po jednej kuli bez zwracania prawdopodobieństwo tego ze wylosowano w ten sposób kule różnych kolorów jest równe . nie wiem dwumian czy co będę bardzo wdzięczny i dziękuję z góry

Qba: |Ω| = 12² |A| = 7*5 + 5*7 P(A) = 2*5*7/12²

Qba: a, sorry, nie zauważyłem, że bez zwracania w takim razie |Ω| = 12*11 i P(A) = 2*5*7/12*11

2: ee nie ma takiej odp

2: możesz jakoś może słownie to wytłumaczyć ?

2: chodzi mi czy można to rozwiązać w jakiś inny sposób ... mianownik ogarniam ale nie resztę

2:

2: to mozze ktos inny ?

2: mimo to będę czekał na rozwiązanie i do jutra może ktoś mnie trochę nakieruję ,.,,,

Qba: na albo najpierw wylosujesz białą (na 7 sposobów), a potem czarną (na 5 sposobów), albo odwrotnie − stąd 2*5*7 a jakie masz odpowiedzi?

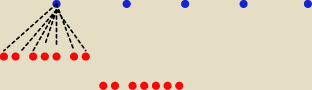
aa: niech niebieskie kropki będą czarne kule a czerwone jako białe kule więc każda czarna może być z jedną z białych czyli A=5*7=35

	35
P(A)=
	132

Qba: aa, wszystko fajnie, tylko jeszcze *2

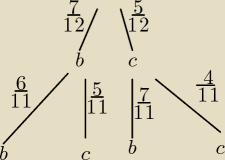
Troja: To jest klasyczne prawdopodobieństwo całkowite. Mnożysz po gałęziach,czyli:

	7		5		5		7		70		35
P(A) =		*		+		*		=		=
	12		11		12		11		132		66

Lub tak jak Qba oznaczasz przestrzeń zdarzeń i zdarzenie sprzyjające wylosowaniu 2 różnych kul ale z doświadczenia wiem, że uczniowie mają bardzo duży problem z pamięciowym rozpisaniem. Dlatego proponuje robić szybkie drzewko

2:

	70
ja mam		jako odp pop
	132

aa: ale jak może być biała i biała kiedy miały być różne

aa: a sorki już wiem

2: tak więc ?

aa: jest ok w moim rozpisaniu brakuje jeszcze 2 bo można pierw losować czarne a potem białe i odwrotnie ( kolejność jest ważna −wariacje)

Qba: 2*5*7/12*11 = 70/132 = 35/66 wszystkie te odpowiedzi są równoważne

2: Troi metoda jest bardzo przejrzysta ... ale dziękuję wszystkim