okrąg AS2731: Punkty A i B należą do okręgu o. Znajdź zbiór środków okręgów wpisanych w takie trójkąty ABP że P należy do okręgu o.

Vax: Na początku 2 lematy: Lemat1) Dwusieczne dwóch kątów wpisanych opartych na tym samym łuku przecinają się w jednym punkcie leżącym na danym okręgu. Dowód: Skoro oba kąty są oparte na tym samym łuku to mają równe miary. Niech dwusieczna jednego kąta tnie dany łuk w punkcie Z, dwusieczna dzieli kąt na dwa równe kąty, skąd łatwo dostajemy, że Z jest środkiem danego łuku, analogicznie dwusieczna drugiego kąta przechodzi przez środek danego łuku, więc istotnie dane dwusieczne tną się w punkcie leżącym na okręgu, cnd. Lemat2) Punkt J jest środkiem okręgu wpisanego w trójkąt ABP. Półprosta PJ przecina okrąg opisany na trójkącie ABC w punkcie X. 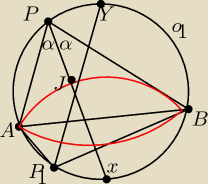Wykaż ze XA=XJ Dowód: https://matematykaszkolna.pl/forum/112176.html ~~~ Przejdźmy do zadania. Weźmy dowolny punkt P leżący na łuku AB jak na rysunku, niech X będzie środkiem łuku AB niezawierającego punktu P, wtedy zgodnie z lematem 1 prosta PJ przechodzi przez X, teraz zgodnie z lematem 2 wiemy, że XA = XJ = XB, czyli A,B,J leżą na pewnym okręgu o środku X, skąd dostajemy, że jeżeli J jest środkiem okręgu wpisanego w ABP to musi leżeć na krótszym łuku AB okręgu o środku w punkcie X, udowodnimy teraz, że wszystkie punkty danego łuku są środkami okręgu wpisanego w trójkąt ABP dla pewnego P, istotnie jeżeli pewne dwa punkty leżą na łuku zawierającym punkt P okręgu o₁ i odcinki łączące dane dwa punkty z X tną dany łuk w punktach J₁,J₂ to wybierając trzeci punkt leżący na krótszym łuku między tymi dwoma punktami widzimy, że łącząc go z X przetnie on nasz łuk w punkcie leżącym między J₁ i J₂, czyli istotnie wszystkie punkty danego łuku są środkami pewnych okręgów wpisanych w dane trójkąty. Analogiczny łuk dostajemy rozpatrując położenie punktu P po przeciwnej stronie łuku AB, zbiór danych środków zaznaczyłem kolorem czerwonym.

rączka: jestem w szoku