planimetria AS2731: Prosta równoległa do boku trójkąta dzieli ten trójkąt na dwie figury o równych polach. Udowodnij że stosunek odcinków wyznaczonych przez tę prostą na jednym lub drugim z pozostałych boków jest równy 1+√2.

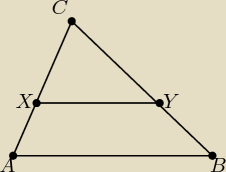
Vax: Trójkąty ABC i XYC są podobne, niech skalą podobieństwa będzie k, wtedy ([XYZ] − pole trojkąta XYZ):

	√2
[XYC] = k2*[ABC] = k2*2[XYC] ⇔ k=
	2

	a√2
I teraz niech bok AC ma długość a, wtedy XC =		więc:
	2

CX		a√2/2
	=
AX		a−a√2/2

	CX
Skąd po prostych przekształceniach		= 1+√2 cnd.
	AX