W ostrosłupie prawidłowym czworokątnym Dawidooooos: W ostrosłupie prawidłowym czworokątnym pole jednej ściany bocznej jest trzy razy mniejsze niż pole jego podstawy. Oblicz objętość ostrosłupa, wiedząc, że długość krawędzi podstawy jest równa 14 cm. Oblicz sinus kąta alfa między sąsiednimi krawędziami bocznymi tego ostrosłupa.

Dawidooooos: Proszę o pomoc zależy mi na czasie

Dagma: Masz, 3 h*a/2=a2, z tego h=28/3 , h−wysokość ściany bocznej Dalej robisz pitagorasa H2=748/9−49, z tego H=7√7/3 Czyli v=1/3Pp*H dalej v wychodzi 1372√7/3 Nie obliczyłam tylko sinusa może ktoś inny Ci jeszcze pomoże

Dagma: Pasuje też zrobić odpowiedni rysunek.

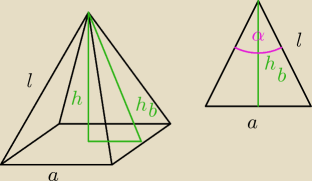
dero2005: P_b → pole jednej ściany bocznej

	a*hb
Pb =
	2

a = 14 P_p → pole podstawy P_p = a² 3*P_b = P_a

3
	a*hb = a2
2

	2		28
hb =		a =
	3		3

	7
h = √hb2 − (a2)2 =		√7
	3

	1372
V = 13a2*h =		√7
	9

l = √(^a₂)² + h_b² = ³⁵₃

	a2
sinα2 =		= 35
	l

α = 73^o44'23'' sinus kąta można policzyć w trójkącie prostkątnym a trójkąt ściany bocznej nie jest prostokątny więc policzyłem sinus połówki kąta i policzyłem cały kąt, nie wiem czy o to ci chodziło

Dawidooooos: dero2005 jestes supeeer nie da się tego opisać dzięki dzięki