zadania pomagacz: Zestaw zadań od m przejrzyjcie te zadania, jeśli na coś wpadniecie dajcie znać, bo na razie to czarna magia w większości zadań http://imageshack.us/photo/my-images/208/skanowanie0001vh.jpg/

ICSP: Co do pierwszego to proponuję wzór wektorowy na pole Drugie trójka jest prostokątny wiec bez problemu Trzecie: Najpierw wzór Herona a później liczysz wszystkie wysokości.

Aga: U mnie zadania są prawie nieczytelne. Zdaje się, że jedno z nich to wyznacz wysokości trójkąta o bokach 5,9,10. p=12 P=√12*3*2*7*=6√14 5h₁=12√14 9*h₂=12√14 10*h₃=12√14

Aga: Już powiększyłam.

	a+b−c
Zad 2.r=
	2

	1
R=		c
	2

re: 7 mogę zrobić chyba ze trzeba wybrane ?!

pomagacz: Nie chodzi o rozwiązanie, wystarczy naprowadzenie na rozwiązanie, i najlepiej dla każdego. Przypominam, że to zestaw od m

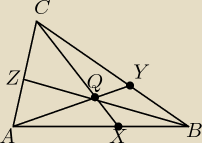Vax: 6) Można z twierdzenia Cevy, nasze proste tną się w jednym punkcie więc:

AX		BY		CZ		CZ		3
	*		*		= 1 ⇔		=
BX		CY		AZ		AZ		2

	2
Można też trochę inaczej, umieśćmy masy 1,2,		odpowiednio w wierzchołkach A,B,C. Wtedy
	3

X,Y będą środkami mas odpowiednio układów punktów (A,B) oraz (B,C), czyli Q będzie środkiem

	CZ
masy trójkąta ABC, skąd wynika, że Z jest środkiem masy układu punktów (A,C) czyli		=
	AZ

	1		3
		=
	2/3		2

m: prosze o zrobienie 7 zadania

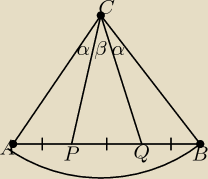Vax: No to 7, trójkąty APC,PQC,QBC mają równe podstawy i tą samą wysokość, więc mają równe pola. Trójkąt APC przystaje do QBC (bkb) więc kąt ACP = kąt QCB. Mamy pokazać jeszcze, że kąt PCQ > kąt ACP, co jest równoważne sinβ>sinα, ale trójkąty APC i PQC mają równe pola więc:

	sinβ		AC
AC*CP*sinα = CP*QC*sinβ ⇔		=		, chcemy więc pokazać, że AC > QC co jest
	sinα		QC

oczywiste (wystarczy chociażby zakreślić łuk AB o środku w C)

m: super dzięki a 9 ktoś umie?

m: cosalfa= −0,1 o co chodzi?