Logika dla matematyka :) Macius: Witam mam takie zadanie [(x+4)(x+2)<=0]⋀[−2(x+2)<=x+2 . Wyznacz wszystkie wartosci rzeczywiste dla x dla ktorych forma zdaniowa jest zdaniem falszywym. Jak to wyliczac. Wiem ze koniunkcja przyjmuje wartosci falszywe gdy p i q sa kolejno 1/0 , 0/1, 0/0 . Teraz jak to rozrysowac i znalezc te x'sy. Rysowac na jednym ukladzie wspolrzednych te wartosci i robic sume zbiorow ? nie chodzi mi o rozwiazanie tylko o metode zrobienia tego zadania.

sushi_ gg6397228: zrob osobno rysunek dla pierwszwego i drugiego dla pierwszego −−> rozwiazanie prawdziwe: ...., rozwiazanie fałszywe: ... dla drugiego−−> rozwiazanie prawdziwe: ...., rozwiazanie fałszywe: ...

Macius: No okej tak zrobilem tylko teraz jak wyliczyc to z tymi falszywym w 3 przypadkach jest falszywe zdanie jak pierwsze (prawda ) drugie (falsz ) itp. tak jak wyzej

sushi_ gg6397228: rozpatrujesz te przypadki, co zostaly podane przez Ciebie 1/0 0/1 i 0/0

Macius: ? sushi chodzi mi wlasnie o wyjasnienie jak to dziala bo rozwiazac te rownania to umiem

Macius: Z pierwszego wychodzi prawda zakres <−4,−2> , drugie prawda <2,+∞) teraz na tym przykladnie wez to jakos wyjasnij

sushi_ gg6397228: 1.falsz (−∞; −4) u (−2, ∞) prawda <−4,−2> 2. falsz (−∞; 2) prawda <2, +∞) 1falsz, 2prawda : (−∞; −4) u (−2, ∞) i <2, +∞) wiec czesc wspolna bedzie <2, +∞) ......

Macius: no ja czaje wsztstko sushi ale odp jest R/{2} jak do tego dojsc

Macius: R/{−2}

Macius:

sushi_ gg6397228: nie zapisales pozostalych warunkow ani czesci wspolnej

Macius: Najlepiej zrob przyklad ja obadam i zobacze jak to dziala (x²−4>0)⋁(−x²+x+30<=0) Bylbym wdzieczny jakbys to po prostu rozpisal zebym zasade zobaczyl jak to smiga.

Macius: w tym drugim przypadku wypisalem wszystkie mozliwosci tj 1/0 (−∞, −5>∪<6,+∞) ; 0/1 <−2,6> ; 1/1 <−5.−2>∪ <2,6> . Odpowiedz jest (−∞,−2)∪(2,+∞) . Jak do tego dojsc jak sprawdzam czesc wspolna tych wszystkich to nie wychodzi tak

Macius: JEST TU KTOS KTO MI TO PO PROSTU WYJASNI JAK TO DZIALA /

Macius: UP

Macius:

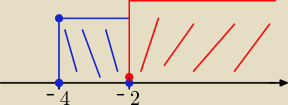
lula: zaznaczasz oba zbiory na wykresie x∊<−4, −2> x∊<−2, +∞) całe zdanie jest prawdziwe dla x spełniającego ten iloczyn czyli częścią wspólną jest x=−2 więc jest fałszywe dla pozostałych x czyli x∊R/{−2}

Macius: czescia wspolna nie jest <−2, +∞) ?

lula: nie pierwsza nierówność jest od −4 do −2 i w tym to punkcie tylko się pokrywają narysuj sobie samemu

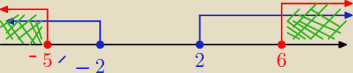
Macius: no to wg mnie to powinno byc wspolny (−∞,−5)∪(6,+∞) Jest tu ktos ogarniety zeby to wytlumaczyc i jakos zapisac bo juz nie mam czasu na to jedno zadanie , a nie bardzo chce sie poddawac...

Macius: Pierwsza nierownosc mowi o x >0 czyli powyzej osi Ox . tj nie <−4, −2> tylko tak jak na rysunku chyba ze cos nie ogarniam to lula wytlumacz

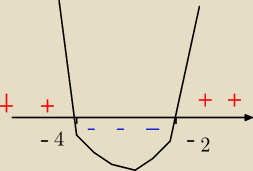
lula: (x+4)(x+2)≤0 x+4=0 x+2=0 x₁=−4 x₂=−2 więc x∊<−4, −2>

lula: −2(x+2)≤x+2 −2x−4≤x+2 −2x−x≤2+4 −3x≤6 x≥−2 więc x∊<−2, +∞)

lula: już ogarniasz?

Macius: lula ogarniam tylko sie nie dogadalismy ty robisz moj pierwszy przyklad a ja na drugim bazuje buehehe ok dziekuje

lula: w drugim przypadku masz sumę dwóch nierówności więc x∊(−∞, −2)u(2, +∞) więc fałsz jest x∊<−2, 2>