zadanie 15 wiesław-rz: krawędź boczna ostrosłupa prawidłowego czworokątnego ma długość 4 cm i jest nachylona dopłaszczyzny podstawy pod kątem 30 stopni. oblicz krawędź podstawy sześcianu, którego obiętość jest równa obiętości ostrosłupa.

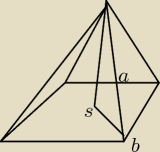
asia: wielokąt foremny to taki który ma wsztstkie boki równe więc podstawą jest kwadrat lub romb Krawędź boczna z wierzchołkiem i środkiem tworzy trójkąt o kątach 30,90 i 60 stopni a więc jest połową trójkąta równobocznego stąd wysokośc H=0,5*4=2cm. odległość od środka podstawy s do b =a√3/2 =2*√3/2 =√3 Objętość sześcianu o boku A = A³ = Objętość ostrosłupa= 1/3* pole podstawy*H a pole podstawy = iloczyn przekątnych podstawy dzielone przez 2 dalej spróbuj sam

wiesław-rz: cały czs próbuje tylko niewiem czy dobrze to robię , a potrzebne mi to jest do pracy kontrolnej to wolałbym żeby było chociaz pare zadań dobrze rozwiązane, a z matematyki orłem nie jestem