trapez wpisany w okrag m: uzasadni że trapez wpisany w okrąg jest tylko wówczas gdy jest równoramienny

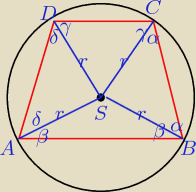
Basia: α+γ = 180−(α+β) β = 180 − 2α − γ δ+γ = 180−(δ+β) 2δ = 180 − β − γ = 180 − (180−2α−γ)−γ = 2α czyli δ = α czyli trójkąty ASD i BSC są przystające czyli AD = BC c.b.d.o

m: to jest dowod +ten trape jest rownoramienn a odwrotnie

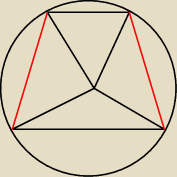
asia: nie umiem ci tego natysować bo nie wiem jak się zaznacza w tym programie kąty. ale dla każdego trapeza wpisanego w okrąg zachodzi zależność iż odległość od środka okregu do dowolego wierzchołka jest=R promień a więc otrzymujesz 4 trójkąty wszystkie równoramienne. zaznacz kąty w każdym trójkącie oraz z właściwości trapezu α+β=180 stopni wyjdzei ci że jest równoramienny

m: podaj gg

Basia: nie; w każdym trapezie suma kątów przy A i C = sumie kątów przy B i D = 180 tu masz udowodnione, że jeżeli to jest wpisane w okrąg (czyli AS=BS=CS=DS=r) ⇒ α=δ ⇒ α+β=δ+β ⇒ kąt przy A = kąt przy B ⇒ trapez jest równoramienny

m: asia gg

m: pogadamz na gg

asia: nie mam gg, podaj maila to ci przyślę rysunek w pdf

asia: Basia dobrze to narysowała

m: chester20malpa.pl

asia: a po małpie co ma być o2?wp?

m: vp