Potrzebne na już!
Monika: Monika: 1. Przedstaw rozwiązanie układu nierówności w prostokątnym układzie współrzędnych i
podaj dwa punkty spełniające ten układ:
2x +y – 2 ≥0
y ≤2
2.Narysuj wykres funkcji y = x2 +1 i omów jej własności.
3.Napisz równanie prostej y = ax +b wiedząc, że f(− 4) = 11 i f(1) = 1.
4.Punkt K = (− 5, 8 ) przesunięto o wektor AB = [ − 2, 4 ] i otrzymano punkt P. Znajdź
współrzędne punktu P.
18 lis 13:18
ICSP: Pierwsze:
2x + y − 2 ≥ 0 ⇔ y ≥ 2x − 2
y = 2x−2
Jest to prosta. Jak zapewne wiesz przez dwa punkty można poprowadzić tylko jedną prostą. Trzeba
więc znaleźć dwa punkty należące do tej prostej.
y = 2x−2
f(1) = 2 −2 = 0 czyli mamy punkt A1(1;0)
f(0) = 0 −2 = −2 czyli mamy punkt A2(0;−2)
teraz rysujesz układ współrzędnych. Rysujesz tą prostą i zakreskowujesz(na skos w którąś
stronę) obszar nad nią.
y ≤ 2 − tutaj rysujesz prostą y = 2(jest ona równoległa do osi OX i podniesiona o 2 jednostki
do góry) i zakreskowujesz(w drugą stronę na skos) obszar pod nią.
Powinien powstać obszar gdzie zakreskowania się pokrywają i to jest właśnie rozwiazanie twojego
zadania.
18 lis 13:23
18 lis 13:24
ICSP: y = x2 + 1
− podnosisz wykres funkcji y = x2 o jedną jednostkę do góry.
D : x ∊ R
Zw : y ∊ <1;+∞)
Brak miejsc zerowych
monotoniczność:
f↓ : x ∊ (−∞;0>
f↑ ; x∊ <0;+∞)
nie wiem co tam jeszcze może być z własności.
18 lis 13:26
Maria : dzięki z waszą pomoco już wiem jak to zrobić

18 lis 13:27
ICSP: Jeszce śpię...
2x + y − 2 ≥ 0 ⇔ y ≥ −2x + 2
czyli rysujesz prostą przechodząca przez punkty : A{0;2) oraz B(1;0). I zakreskowujesz obszar
nad nią.
18 lis 13:28
Monika: dobra a dlaczego w 1 o 2 jednoski w góre
18 lis 13:28
Monika: y = x2 + 1 − podnosisz wykres funkcji y = x2 o jedną jednostkę do góry. D : x ∊ R Zw : y ∊
<1;+∞) Brak miejsc zerowych monotoniczność: f↓ : x ∊ (−∞;0> f↑ ; x∊ <0;+∞) nie wiem co tam
jeszcze może być z własności.
Które to zad?
18 lis 13:30
ICSP: Drugie.
18 lis 13:35
Monika: czekaj a w 1 to jak o 2 jednoski w góre to na 4
18 lis 13:37
ICSP: nie. PO prostu narysuj prostą y = 2 i zakreskuj obszar pod nią.
18 lis 13:42
Monika: no czyli to liczy większe niż 2
18 lis 13:46
Monika: a ta prosta to jak y= 2x−2
18 lis 13:46
ICSP: mniejsze.
18 lis 13:46
ICSP: masz nierówność y ≤ 2
wstawmy 1 oraz 3
1 ≤ 2 − prawda
3 ≤ 2 − sprzeczność.
Czyli zakreskowawszy obszar pod wykresem.
18 lis 13:47
Monika: zgadza sie
18 lis 13:48
Monika: pogubiłam sie a to co?
Jeszce śpię... 2x + y − 2 ≥ 0 ⇔ y ≥ −2x + 2 czyli rysujesz prostą przechodząca przez punkty :
A{0;2) oraz B(1;0). I zakreskowujesz obszar nad nią.
18 lis 13:50
ICSP: to jest poprawiona treść pierwszego zadania.
Na początku źle przeszedłem z postaci : 2x + y − 2≥ 0
18 lis 13:50
Monika: napisz mi w całości jak to ma być
18 lis 13:51
ICSP:
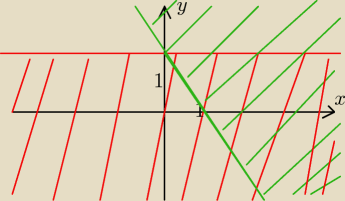
18 lis 13:53
Monika: coś mi to nie wychodzi
18 lis 13:53
Monika: to 1 mamy z głowy
18 lis 13:55
Monika: 2x + y − 2 ≥ 0 ⇔ y ≥ 2x − 2 y = 2x−2 Jest to prosta. Jak zapewne wiesz przez dwa punkty można
poprowadzić tylko jedną prostą. Trzeba więc znaleźć dwa punkty należące do tej prostej. y =
2x−2 f(1) = 2 −2 = 0 czyli mamy punkt A1(1;0) f(0) = 0 −2 = −2 czyli mamy punkt A2(0;−2)
coś mi tu nie pasuje
18 lis 13:56
ICSP: 3.
y = ax +b
f(1)=1
f(−4) = 11
podstawiamy współrzędne punktów
1 = a + b
11 = −4a + b
układ równań jest prosty. Rozwiążesz go już sama.
y = −2x + 3
18 lis 13:59
Monika: czekaj trzecie sama robiłam to napisze a ty spr
18 lis 14:00
ICSP: 2x + y − 2 ≥ 0 ⇔ y ≥ 2x − 2 y = 2x−2 Jest to prosta. Jak zapewne wiesz przez dwa punkty można
poprowadzić tylko jedną prostą. Trzeba więc znaleźć dwa punkty należące do tej prostej. y =
2x−2 f(1) = 2 −2 = 0 czyli mamy punkt A1(1;0) f(0) = 0 −2 = −2 czyli mamy punkt A2(0;−2) −
ŹLE
Jeszce śpię... 2x + y − 2 ≥ 0 ⇔ y ≥ −2x + 2 czyli rysujesz prostą przechodząca przez punkty :
A{0;2) oraz B(1;0). I zakreskowujesz obszar nad nią. − DOBRZE
18 lis 14:00
Monika: 3
y=ax=b − równanie liniowe prostej
f(−4)=11 i f(1)=1
(podstawiam do wzoru y=ax+b)
f(−4)=11 i f(1)=1
f(x)=−4a+b=11 f(x) = 1*a+b=1
(powstaje układ równań)
−4a+b=11
a+b=1
b=11+4a
a+11+4a=1
b=11+4a
5a=1−11
b=11+4a
5a= −10/:5
a= −2
b=11+4*( −2)
a= −2
b=11−8
a= −2
b=3
równanie prostej f(x) = −2x+3
18 lis 14:07
ICSP: Bardzo dobrze. CO prawda można było przemnożyć przez −1 dowolne równanie i metoda przeciwnych
współczynników ale podstawiania też dobra.
18 lis 14:08
Monika: No dobra a możesz mi zrobić tak dokładnie żebym to przepisała to 1 i 2 bez pomyłki bo w tym
przepisywaniu się nie łapie
18 lis 14:10
ICSP: K(−5;8)
AB[−2;4]]
to chyba najprostsze zadanie. Po prostu dodajemy odpowiednio
P(−5 −2 ; 8 + 4)
już sobie poradzisz z dokończeniem.
18 lis 14:10
ICSP: y ≥ −2x + 2
y ≤ 2
i robisz rysunek.
Tyle z pierwszego.
18 lis 14:11
ICSP: drugie jest napisane ładnie.
18 lis 14:11
Monika: a to pierwsze ma być z tabelą jeszcze

18 lis 14:12
ICSP: może być ale nie musi. Ja rysowałem wykresy funkcji liniowych bez tabelki i mi uznawała. Zależy
od nauczyciela.
18 lis 14:13
Monika:
x −1 0 1
y 4 2 0
czy tak jest ok
18 lis 14:17
Monika: nie czaje 2 zad
18 lis 14:23
Monika: nie wychodzi mi 2 zad ( wykres)
18 lis 14:32
Monika: ICSP zrób mi wykres do 2
18 lis 14:38
Monika: dzięki za pomoc
18 lis 14:59
Andrzej: Monika. 2 zadanie to jest tak jak tutaj :
https://matematykaszkolna.pl/strona/1379.html
U ciebie jest y = x
2 +1 , czyli parabola y =
x
2 podniesiona o jedną jednostke do góry, a w tym zadaniu masz y = x
2 − 4 czyli parabola y =
x
2 obnizona o 4 jednostki w dól.
18 lis 18:54
18 lis 18:56
Monika: nie czaje bazy
18 lis 19:12
Monika: Miało nie być miejsc zerowych a wychodzi że są
18 lis 19:13
Monika: i chyba trzeba obliczyć Δ, p i q
18 lis 19:14
ICSP: a niby gdzie masz miejsca zerowe?
18 lis 19:20
Monika: sorki ale i tak wykres mi nie wychodzi
18 lis 19:22
Monika: Pomocyy

18 lis 21:52



