prawdopodobieństwo małysz: W grupie 30 osób 20 gra w brydża, 15 gra w szachy, a trzy osoby nie grają w żadną z tych gier. Oblicz prawdopodobieństwo tego, że: a) wybrana losowo osoba z tej grupy gra zarówna w brydża, jak i w szachy, b) dwie wybrane losowo osoby nie grają w żadną z tych gier

małysz: Ktoś czai to?

Vizer: Nie wiem czy dobrze rozumiem, ale osób grających jest więcej niż w ogóle wszystkich osób.

sushi_ gg6397228: bo jest jeszcze czesc wspolna

małysz: No tak, część umie w to i w to.

Vizer: Hmm faktycznie tak może być, nie załapałem na początku.

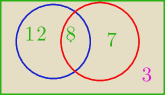
sushi_ gg6397228: 30−3=27 w cos umieja grac 20+15− 27 = 8 czesc wspolna 20−8=... 15−8=...

małysz: Czyli a) 8/30 b) 3/30 Nie, ie wiem co dalej...

wik: skrocic ulamki

b.: b) jest bardziej skomplikowane, bo losujemy 2 osoby, a nie jedna. mozna policzyc to p−stwo mnozac p−stwo wylosowania jednej niegrajacej osoby, a nastepnie kolejnej z pozostalych 29

wik: ale domyslam sie, ze losowano 2 osoby, to ilosc kombinacji 2 z 3 = 3

wik: Ω to sa kombinacje 2 el. z 30

ytyt: ββγγ

ytyt: Ω mam to w dupie dziwko

hfgfrfgfrgrgdr: α⇔βγδπΔΩ∞≤≥∊⊂ggffddΩΩΩΩΩΩΩvdcd csdwdrdsdfefdfssddffdfedsdfrgfsdsde fggggffdcdcdfrf fvfffffvxdbgdfd fdvfev hb gbfgbhghngbtgtb rgrgrffpfjffvvfvf hytggtt5grtgrggrgrgr gfggfggrgfggrgfr fgrgergrefr uruyhrtgrffgrtrbfrgtrgrrgrurbgrg yrgfrfrggrhrrrhhrhrrrrr jjjnhnhhynhbgh tgtbgthggdgfgbfgfbdsje gtbtgtgrtbryrhdgrrbythfhfhfhfjefwrwuwoqlaj≤∞ΔΔΔΔππγδ→→→→→mjmjjmjthmjmghhytrvrttrtrerr5frrfr ggtgrgerrgtrghftry6tffrgrgtgggg hghhftgthgrtgfgrfggrttrhrgffdrrrrgrrgrrgrhrrrfr yrggrfrgfrfrf nhrgrgdrgrrggrrfrfgghgyghfhkowsdvv tgrggtgrtggrggrgtrgrgrgrhryjrgrrurjqwweertyuioppasfghjkllzxcvbnmmm fgfgvftrrff gffgf hf bgfbgbgbhthfrgthtutjthtgtf hgnhghgbghgnhggngbggbghgytgtutqwertuioppasasdfghhhhhhjkl\zzzzzzxxxxxxxxxxxccccccc