pomoc kkkkkkj: w urnie jest 14 kul bialych i 10 kul czarnych.wylosowano 2 razy po 1 kuli bez zwracania. Prawdopodobieństwo tego ze wylosowano w ten sposób kule różnych kolorów jest równe?

Eta: |Ω|= 24*23 A= (b,cz) (cz,b)} |A|= 14*10+10*14= 2*10*14 P(A)= ................

kkkkkkj: i co to równa się 280 i to koniec?

kkkkkkj: a co to jest b icz?

kkkkkkj: Wszystkie: {14+10\choose 1}{14+10−1\choose 1}=552 A − najpierw kula biała, potem czarana: P(A)={14\choose 1}{10\choose 1}=140 Czyli (na ile sposobów można wylosować białą kulę)*(na ile czarną). B − odwrotna kolejność (ale wynik się nie zmieni, bo mnożenie jest przemienne). Stąd P(A\cup B)=\frac{2\cdot 140}{552}=\frac{35}{69} W tym zadaniu to czy losowanie było bez zwracania, czy ze zwracaniem nie ma znaczenia dla wyniku. Gdyby obie kule miały być tego samego koloru, miałoby to znaczenie, bo wtedy, bez zwracania za drugim razem w urnie byłaby "jedna kula mniej do wyboru

kkkkkkj: dobrze jest to?

Aga: To zadanie łatwo rozwiążesz z drzewkami. Metoda Ety prowadzi szybko do wyniku i jest poprawna. Ta druga nie jest dla mnie,bo nie znam takich zapisów.

kkkkkkj: a pomozesz bo mnie nie było nha lekcjach i mam zaległości

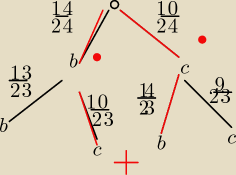
Aga: 14− liczba kul białych 10− liczba kul czarnych

	14		10
razem 24.Prawdopodobieństwo wylosowania kuli białej wynosi		, a czarnej
	24		24

Jak jedną wyciągniemy, to odkładamy ją na bok Zostanie23. jak wylosowano białą to będzie 13 białych i 10czarnych

	13		10
Prawdopodobieństwo wylosowania białej=		, a czarnej		4
	23		23

Jak wylosowano czarną to będzie 14 białych i 9 czarnych

Aga:

	14		10		10		14
P=		*		+		*
	24		23		24		23

kkkkkkj: i tego juz nie trzeba liczyc dalej tak?

niusia: DOBRZE TO JEST ROZWIąZANE