Liczby zespolone
ICSP: Potrafi ktoś rysować liczby zespolone?
mam np cos takiego:
|z−3+4i| < 5
wiem że to będzie koło tylko nie potrafię wyznaczyć srodka.
16 lis 20:14
Sławek:
Interpretacja geometryczna nierówności z modułem typu
|z−z0| < r
to będzie koło o promieniu r i środku w punkcie z0 bez okręgu o promieniu r (bo nierówność
jest ostra tzn. <)
czyli w Twoim zadaniu to będzie tak
|z−3+4i| < 5
|z−(3−4i)| < 5
16 lis 20:27
ICSP: Dziękuję bardzo

16 lis 20:30
ICSP: a teraz taki przykład:
Re(iz + 2)≥ 0
16 lis 20:32
Sławek:
Re(iz+2)≥0 ⇔ Re[i(x+iy)+2] ≥ 0 ⇔ Re[ix+i2y+2] ≥ 0 ⇔ Re[ix − y+2]≥0
⇔ Re[−y+2 + ix] ≥ 0 ⇔ −y+2 ≥ 0 ⇔ y ≤ 2
16 lis 21:00
ICSP: chyba rozumiem

czyli : imz
2 < 0 ⇔ Im(x+yi)
2 < 0 ⇔ IM(x
2 − y
2 + 2xyi) < 0 ⇔ 2xy < 0 ⇔ xy< 0 czyli
zamalowuje drugą i czwartą ćwiartkę bez osi?
16 lis 21:03
Sławek:
nie
16 lis 21:04
Sławek:
nie zauważyłem, że wpisałeś już nowe zadanie
16 lis 21:06
ICSP: tzn że dobrze?
16 lis 21:06
Sławek:
moim zdaniem tak
16 lis 21:12
ICSP: dziękuję

Wreszcie coś mi zaczęło wychodzić

Jutro jeszcze przysiądę i zobaczymy jak mi pójdzie reszta
przykładów

16 lis 21:13
Trivial:
Hej
I. 
16 lis 21:13
ICSP: pomoże ktoś z takim przykładem:
(z−i) = z−1
to w nawiasie to ma kreskę na górze.
17 lis 14:43
b.: podstaw z = x+iy (x,y ∊ R) i rozwiaz
17 lis 14:52
ICSP: aaa
to x,y musi ∊ R

czyli wychodzi mi :
| | 1−i | | i + 1 | |
y = |
| = |
| to nie należy do rzeczywistych wiec nie da sie tego narysować? |
| | 2i | | −2 | |
17 lis 14:54
b.: to znaczy, ze cos zle rozwiazujesz. podstaw tak jak napisalem i posortuj osobno czesc
rzeczywista, osobno czesc urojona po obu stronach. czesci rzeczywiste obu stron musza byc
rowne i tak samo urojone, co da dwa rownania (liniowe) na x,y
17 lis 14:59
ICSP: (x − yi − i) = x + yi − 1
−2yi = −1 + i
2yi = 1 − i
nie wiem gdzie błąd robię.
17 lis 15:03
Sławek:
Cytat z "Algebra liniowa" Jurlewicz, Skoczylas
Odp. Rozdz. I, Zad. 1.4c) "zbiór pusty"
17 lis 17:36
ICSP:
gdzie ź to sprężenie.
Osobiście stawiam na okrąg o promieniu 4 i środku w punkcie (0;0) ?
17 lis 20:47
Godzio: z ≠ 0
4 = z * ź = |z| /
2
16 = x
2 + y
2
Ok, tylko uwzględnij z ≠ 0

17 lis 20:49
ICSP: | | 1+iz | |
a Godziu coś takiego : Im |
| = 1 |
| | 1−iz | |

Na to już zupełnie nie mam pomysłu

17 lis 20:52
Godzio:
z = x + yi
| 1 + iz | | 1 + xi − y | | 1 + y + xi | |
| = |
| * |
| = |
| 1 − iz | | 1 − xi + y | | 1 + y + xi | |
| (1 + xi)2 − y2 | | 1 − x2 + 2xi − y2 | |
| = |
| = |
| (1+ y)2 − (xi)2 | | 1 + 2y + y2 + x2 | |
| 1 − x2 − y2 | | 2x | |
| + |
| i |
| ... | | x2 + y2 + 2y + 1 | |
| | 2x | |
lm(...) = |
| = 1 |
| | x2 + y2 + 2y + 1 | |
itd.
17 lis 20:55
ICSP: czyli mam narysować coś takiego :
| 2x | |
| = 1  |
| x2 + y2 + 2y + 1 | |
17 lis 21:32
Godzio:
No po przekształceniach, na oko okrąg jakiś
17 lis 21:33
ICSP: no to x ≠ 0 oraz y ≠ −1
2x = x2 + y2 + 2y +1
x2 − 2x +1 +(y+1)2 = 1
(x−1)2 + (y+1)2 = 1
?
17 lis 21:36
Godzio: 
17 lis 21:38
ICSP: Już zaczynam rozumieć to rysowanie

Kolokwium się zbliża i trzeba się w końcu do roboty wziąć

17 lis 21:43
Godzio: A żebyś wiedział kolokwium ... zbliża się hmmm ... wtorek
17 lis 21:44
ICSP: hmm skąd wiesz

17 lis 21:51
Godzio:
A wiesz, też mam wtedy

17 lis 22:07
ICSP: To może jeszcze o tej samej godzinie mamy

17?
17 lis 22:10
Eta:
I z tym samym wykładowcą ?

17 lis 22:15
ICSP: kto wie

17 lis 22:50
Godzio: 13:15

17 lis 22:53
ICSP: Znowu się za to zabieram i nie jestem pewien takiego twierdzenia.
z * ź = |z|
2
Jeżeli jest prawdziwe to wtedy równanie:
z*ź + (5+i)z + (5−i)ź + 1 = 0
mogę sprowadzić do postaci (x+5)
2 − (y−1)
2 = 25

ź oznacza sprężenie.
18 lis 18:53
ICSP: Trivial proszę

Jeszcze tylko 6 podpunktów zrysowania

18 lis 19:08
Trivial: Podstaw z = (x−iy) i wymnażaj.

18 lis 19:09
ICSP: tzn podstawiłem. Tylko nie jestem pewien czy dobrze mi wyszła ta ostatnia postać

18 lis 19:10
18 lis 19:14
ICSP: genialne

Możesz mi jeszcze powiedzieć jak oznaczamy osie?
Czy zawsze są liczby rzeczywiste czy trzeba czasem wprowadzić jednostkę urojoną?
np. taki przykłąd:
|z−3+4i| = 1
|z − (3 − 4i)| = 1
okrąg o środku w punkcie 3;−4i oraz promieniu 1
Na osi y wstawiam jednostkę urojoną?
18 lis 19:18
Trivial: Nie można tak oszukiwać. Podstawiaj z = (x+iy) i licz. Nie wyjdzie wcale okrąg.

18 lis 19:23
ICSP: |x+yi −3 + 4i| =1
|x−3| + i(y+4)| = 1
mógłbyś małą podpowiedź dać?
18 lis 19:26
Trivial: Sorry. Coś mi się pomieszało i zacząłem sam oszukiwać. Tak. To będzie okrąg taki jak mówisz.
18 lis 19:29
Trivial: Powodzenia z zadankami. Ja idę.

18 lis 19:31
ICSP: No to zaczynamy kolejne:
co w takich przypadkach robić?
podstawiać z = x+yi oraz usuwać niewymierność z mianownika?
Nawet jeżeli podstawię to będę miał w mianowniku 3 wyrazy?
Jak ma trzy wyrazy to porządkować to części rzeczywistych i urojonych a następnie przemnożyć
przez sprężenie tej liczby która mi wyjdzie?
18 lis 19:33
Monika: No to zostaliśmy sami z zadankami
18 lis 19:33
Trivial:
| z−2i | | x + i(y−2) | |
| = |
| = ...  lecę. |
| z+1 | | (x+1) + iy | |
18 lis 19:35
ICSP: To taki myk tutaj jest

18 lis 19:42
ICSP: jestem w momencie:
| | x2 + x + y2 − 2y + i(y−2x−2) | |
| |
| | = 1 |
| | x2 + 2x + 1 + y2 | |
nie mam dalej pomysłu

18 lis 19:51
ICSP: chwilkę mam inny pomysł

18 lis 19:55
ICSP: |x + i(y−2)| = |(x+1) + yi|
i nie wiem co zrobić gdy dwa moduły są równe

18 lis 20:03
Sławek:
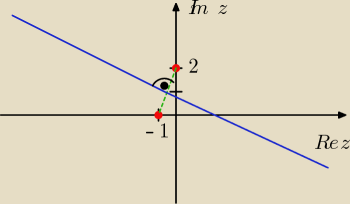
A ja bym zaproponował coś takiego:
| | z1 | | |z1| | |
najpierw skorzystanie z własności : | |
| | = |
| z2 ≠ 0 |
| | z2 | | |z2| | |
czyli
a potem
|z−2i| = |z+1| ⇔
|z−2i| = |z−(−1)|
Będzie to symetralna odcinka o końcach w punktach −1 oraz 2i
18 lis 20:04
ICSP: Dziękuję
Sławku. JUz teraz wiem jak się z tymi modułami robi

18 lis 20:07
ICSP: zostały mi jeszcze dwa ostatnie przykłady:
2 ≤ |iz−5| < 3
podstawiam:
|ix − y − 5| i tutaj nie wiem jak to zinterpretować.
z tego wnioskuje że:
|z+i| ≥ |z
2+1|
ale nie wiem co dalej.
19 lis 14:18
ICSP: Godziu spojrzysz?

19 lis 14:41
Godzio: Spojrzę

19 lis 15:31
Godzio:
ICSP ... BANAŁ !

z
2 + 1 =

?

Co do pierwszego. To jest pierścień o środku w .... zawierający się pomiędzy okręgami o środku
w ... o promieniach 2 i 3
19 lis 15:34
Monika: ISCP co z moim wykresem do zad 2
19 lis 15:45
Godzio: Monika, ICSP chyba poszedł, więc jak chcesz to daj to co trzeba narysować to to
zrobię
19 lis 15:46
Monika: Dodałam nowe
19 lis 16:00
ICSP: ale godziu:
|−ix −y − 5| podstawiłem i to ma być niby okrą o środku (5;−1)
19 lis 16:13
ICSP: Trivial dziękuje

19 lis 16:19
Godzio: x = 0. y = −5 tak ?
19 lis 16:22
ICSP: tak

19 lis 16:23
19 lis 16:26
ICSP: kończę z rysowaniem

| | π | |
mam teraz przedstawić liczbę : 1 + itgα α∊(0; |
| ) w postaci trygonometrycznej. Liczę więc |
| | 2 | |
moduł.
czyli liczba jest w postaci:
| 1 | |
| (cosα + isinα)  |
| cosα | |
To jest prawidłowe rozwiązanie?
Jeśli tak to jak zrobić taki przykład:
| | π | |
sinα + icosα α ∊ (0; |
| ) |
| | 2 | |
19 lis 17:15
AC:
cosβ + isinβ gdzie β=π/2 −α
19 lis 18:02
Sławek:
| | 5 | |
2 ≤ | iz−5| < 3 ⇔ 2 ≤ | i(z− |
| ) | < 3 ⇔ 2 ≤ | i(z+5i) | < 3 |
| | i | |
⇔ 2 ≤ | i | * |(z+5i) | < 3 ⇔ 2 ≤ 1 * |(z − (−5i) | < 3
⇔ 2 ≤ |(z − (−5i) | < 3
19 lis 18:22
Sławek:
| | z+i | | |z+i| | | |z+i| | |
| |
| | ≥ 1 ⇔ |
| ≥ 1⇔ |
| ≥ 1 |
| | z2+1 | | |z2+1| | | |z2+1| | |
| |z+i| | | |z+i| | |
| ≥ 1 ⇔ |
| ≥ 1 |
| |(z+i)(z−i)| | | |z+i|*|z − i| | |
| | 1 | |
⇔ |
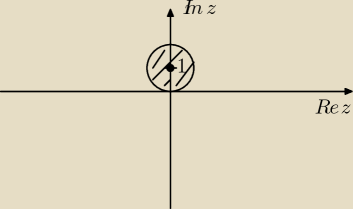
| ≥ 1 ⇔ |z − i| ≤ 1 |
| | |z − i| | |
19 lis 18:28
Sławek:
19 lis 18:34
ICSP: Dziękuję
Sławku i
AC za pomoc

19 lis 19:17
ICSP: ale czegoś tu nie rozumiem
| | π | |
cosβ + isinβ gdzie β∊ |
| − α |
| | 2 | |
i to jest już odpowiedź? Jeśli tka to jakaś dziwna bo nigdy się z takim sposobem nie spotkałem.
Nie istnieje inny sposób na rozwiązanie tego?
19 lis 19:22
Godzio:
To jest typ zadania "super proste" tylko trzeba napisać tą banalną obserwacje

19 lis 20:11
ICSP: i tylko tyle?
19 lis 20:12
Godzio: Tak
19 lis 20:12
ICSP: ciekawy przykład

19 lis 20:16
Godzio:
Nudny, nie ma co liczyć

19 lis 20:23
ICSP: W takim razie
Godziu proszę:
| | π | | π | |
(sin |
| +icos |
| ) 24 dla ciebie  |
| | 6 | | 6 | |
19 lis 20:28
Sławek:
Moje trzy grosze
z = x + iy = |z|(cosφ + isinφ)
z = sinα + i cosα
|z| =
√sin2α + cos2α = 1
zatem
| | π | | π | |
z = 1*[cos( |
| − α) + i sin ( |
| − α)] |
| | 2 | | 2 | |
19 lis 20:30
AC:
Nie ma co liczyć
wynik 1
19 lis 20:45
ICSP: | | π | | π | |
cos |
| − isin |
| to nie jest postać trygonometryczna? |
| | 4 | | 4 | |
19 lis 21:02
:): Jest bo zauważ że cos(−x)=cosx a sin(−x)=−sinx
| | π | | π | | π | | π | |
czyli cos(− |
| ) + sin(− |
| ) = cos |
| − sin |
| . |
| | 4 | | 4 | | 4 | | 4 | |
19 lis 23:27
Gaga: jak narysować?
Rez + Imz = 0


?
3 gru 15:37
aaa: |(z−i)/(z−1)| >1 where z = x+iy pomoże ktoś?
22 kwi 22:33
zajączek wielkanocny:
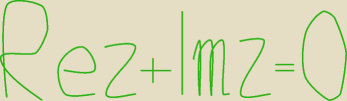
Mnie się udało narysować

22 kwi 22:37
ICSP: |z − i| > |z − 1|
Czyli odległość od punktu (0 ; −1) musi być większa od odległości od punkt (1 ; 0 )
22 kwi 22:38
ICSP: pierwszy punkt (0 ; 1)
22 kwi 22:42
Godzio:
ICSP uczy się liczb zespolonych

22 kwi 22:47
ICSP: 
22 kwi 22:53

 czyli : imz2 < 0 ⇔ Im(x+yi)2 < 0 ⇔ IM(x2 − y2 + 2xyi) < 0 ⇔ 2xy < 0 ⇔ xy< 0 czyli
zamalowuje drugą i czwartą ćwiartkę bez osi?
czyli : imz2 < 0 ⇔ Im(x+yi)2 < 0 ⇔ IM(x2 − y2 + 2xyi) < 0 ⇔ 2xy < 0 ⇔ xy< 0 czyli
zamalowuje drugą i czwartą ćwiartkę bez osi?
 Wreszcie coś mi zaczęło wychodzić
Wreszcie coś mi zaczęło wychodzić  Jutro jeszcze przysiądę i zobaczymy jak mi pójdzie reszta
przykładów
Jutro jeszcze przysiądę i zobaczymy jak mi pójdzie reszta
przykładów 

 czyli wychodzi mi :
czyli wychodzi mi :

 Na to już zupełnie nie mam pomysłu
Na to już zupełnie nie mam pomysłu


 Kolokwium się zbliża i trzeba się w końcu do roboty wziąć
Kolokwium się zbliża i trzeba się w końcu do roboty wziąć 


 17?
17?



 ź oznacza sprężenie.
ź oznacza sprężenie.
 Jeszcze tylko 6 podpunktów zrysowania
Jeszcze tylko 6 podpunktów zrysowania 


 Możesz mi jeszcze powiedzieć jak oznaczamy osie?
Czy zawsze są liczby rzeczywiste czy trzeba czasem wprowadzić jednostkę urojoną?
np. taki przykłąd:
|z−3+4i| = 1
|z − (3 − 4i)| = 1
okrąg o środku w punkcie 3;−4i oraz promieniu 1
Na osi y wstawiam jednostkę urojoną?
Możesz mi jeszcze powiedzieć jak oznaczamy osie?
Czy zawsze są liczby rzeczywiste czy trzeba czasem wprowadzić jednostkę urojoną?
np. taki przykłąd:
|z−3+4i| = 1
|z − (3 − 4i)| = 1
okrąg o środku w punkcie 3;−4i oraz promieniu 1
Na osi y wstawiam jednostkę urojoną?


 lecę.
lecę.



 A ja bym zaproponował coś takiego:
A ja bym zaproponował coś takiego:



 z2 + 1 =
z2 + 1 =  ?
?  Co do pierwszego. To jest pierścień o środku w .... zawierający się pomiędzy okręgami o środku
w ... o promieniach 2 i 3
Co do pierwszego. To jest pierścień o środku w .... zawierający się pomiędzy okręgami o środku
w ... o promieniach 2 i 3


 Może ktoś wytłumaczyć?
Może ktoś wytłumaczyć?









 ?
?
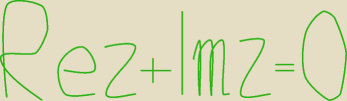 Mnie się udało narysować
Mnie się udało narysować 

