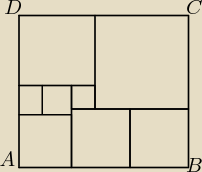
Zadanie z konkursu Złota Żabka dla kl.V i VI Jolka: Zadanie 7 (7 pkt) Żabki podzieliły prostokąt ABCD na różne kwadraty (patrz rysunek). Teraz wiedząc, że bok AB prostokąta ma długość 32 cm, chcą obliczyć długość boku AD tego prostokąta. Pomóż żabkom obliczyć długość tego boku. Rysunek trochę niedokładny, oryginał http://www.ekos.edu.pl/konkurs/downloads/2010/zabka_matematyka_I_etap2010-11.pdf Może ktoś ma pomysł na rozwiązanie

Jolka: Zna ktoś inny sposób rozwiązania tego zadania niż metoda prób i błędów?

mag:

Panko: Liczone na kolanie AD=29 Oznaczmy AD=b AB= x+y+y kolejne boki od wierzchołka A do B 1. 32 =x+2y AD =x + x/2 + ( b−3/2 x) licząc od wierzchołka A do D DC= (b−3/2x) +(32−(b−3/2x)) licząc od D do C CB= (b−y) +y licząc od C do B Stąd 2. 32−(b−3/2x) =b−y Oznaczmy r bok tego naj mniejszego kwadratu( centralny) Rzutując go na bok DC jest r=(b−3/2x) −x Rzutując go na bok AD jest r=(b−y) −( b−3/2x) Porównując dwa powyższe jest 3. b=4x−y Rozwiązując układ równań 1. 2. 3. dostajemy b=29 Podsumuję Narobiłem się jak wół, no chyba jak osioł.To nie tak ma być. Polecam dokładnie sprawdzić, bo powstawało na kolanie.