Pomocy Angelika: rozwiąż nierówność: a) (x−3)(x+2)≥0 b) x³+3x²+2x−6<0

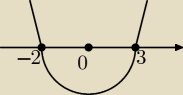
Goli: (x−3)(x+2)≥0 Czyli:x−3=0 x+2=0 x=3 x=−2 Znaczysz odpowiedzi na osi liczowej, następnie rysujesz parabole ramionami do góry gdyż współczynik kierunkowy tej nierówności jest większy od 0. I już kończysz zadanie odczytem przedziałów w którym x≥0. Odp. x∊(−∞,−2>∪<3,+∞)

Aga: Odczytujesz ,gdzie y≥0

Goli: x³ +3x² +2x−6<0 Szukasz przez jaki dwumian ten wielomian jest podzielny. Aby to zrobić patrzysz na wyraz wolny najpierw wypisujesz jego wszystkie dzielniki: {−1,1,−2,2,−3,3} a nastepnie spawdzasz dla jakiego z nich wielomian się zeruje. Kolejno dzielisz (x³ +3x² +2x−6):(x−1)=x²+4x+6 Wniosek z tego, że wielomian x³ +3x² +2x−6= (x²+4x+6)(x−1) (x²+4x+6)(x−1)<0 Wyliczasz x.W pierwszym jest równanie kwadratowe, więc strosujesz wzór na delte Δ=b²−4ac Δ=16−24 Delta wychodzi mniejsza od zera czyli równanie to nie ma rozwiązania biorąc pod uwagę liczby rzeczywiste. Wniosek ta nierównośc nie ma rozwiązania. Jest sprzeczna.

chmy: (x−2)(x+3)<0

asia: (x−2)(x+3)<0

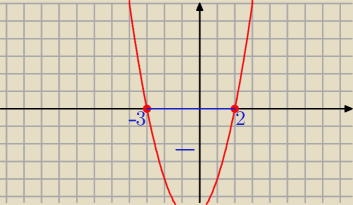
Janek191: ( x − 2)*(x + 3) < 0 ( x + 3)*(x − 2) < 0 x₁ = − 3 x₂ = 2 Ramiona paraboli są skierowane ku górze,więc x ∊ ( − 3; 2 )