Ciągłość Godzio: Funkcja wypukła spełnia warunek: Dla x,y ∊ (a,b) i λ ∊ (0,1) zachodzi: f(λx + (1 − λ)y) ≤ λf(x) + (1 − λ)f(y). Uzasadnić, że każda funkcja wypukła jest ciągła. Mogę to robić z def. Cauchy'ego ? ∀ε> 0 ∃δ>0 ∀x( |λx + (1 − λ)y − λx₀ + (1 − λ)y₀| < δ ⇒ |f(λx + (1 − λ)y) − f(λx₀ + (1 − λ)y₀)| < ε ) Nie jestem pewien czy tak można to zapisać ?

Godzio: Odświeżam

b.: możesz próbować z def. C. −− ale to co napisałeś to nie jest ta definicja. jak już napiszesz definicję, to ustalasz sobie x₀∊(a,b) oraz ε> 0 i próbujesz pokazać, że istnieje odpowiednia delta... to nie jest najłatwiejsze zadanie. spróbuj sobie najpierw wyobrazić na rysunku, czemu funkcje wypukłe (na przedziale otwartym!) są ciągłe, a potem spróbuj zapisać formalnie swoje obserwacje możesz też poszukać funkcji wypukłej f: [a,b] −> R, która nie jest ciągła (zwróc uwage na przedzial: jest domkniety), to moze tez troche pomoc zrozumiec, co sie dzieje

b.: jeszcze co do rysunku: zastanów się nad interpretacją geometryczną podanej definicji wypukłości (oczywiście jeśli jeszcze nie znasz tej interpretacji)

Eta: @Godzio Wszystkiego najlepszego z okazji wczorajszej rocznicy urodzin Ponad to życzę abyś wykształcił w przyszłości co najmniej dziesiątki "Vaxów"

Godzio: Tak patrząc na rysunek, wartości dla każdego argumentu z przedziału gdzie funkcja jest wypukła są mniejsze od wartości prostej przechodzącej przez wartości w a i b więc: Jeśli prosta f(λ) = λf(x) + (1 − λ)f(y) (λ ∊ (0,1) ) ciągła i ma "odpowiedniki" pod swoimi wartościami w wartościach danej funkcji wypukłej to z tego wychodzi że f jest też ciągła, nie wiem czy dobrze to rozumuje ?

Godzio: Hehe, dziękuję Eta !

Eta:

rumpek: Również dołączam się do "spóźnionych" życzeń Tak wczoraj myślałem, o tej 13−stce, lecz nie byłem pewien Ale za to chyba coś kojarzę, że Eta ma 24 ? Ale jeszcze raz − wszystkiego dobrego Godzio

Godzio: Dzięki, w ramach prezentu możecie mi zrobić to zadanie Bo się w nie wkopałem na zajęciach i muszę zrobić

b.: pierwsze 2 wiersze: no prawie ok, chociaż w a i w b f nie jest określona (to są końce przedziału), trzeba było jakichś innych liter użyć na punkty wewnątrz (a,b) dalsza część jest juz dla mnie niezrozumiala: "odpowiedniki"? no nic, wszystkiego dobrego z okazji urodzin i dobranoc

b.: mozesz sprobowac nie wprost (nie jest to konieczne, ale moze nieco latwiej bedzie)

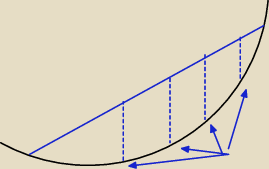
Godzio: O te odpowiedniki mi chodziło

Godzio: Na pewno nikt nie jest w stanie mi to udowodnić ?