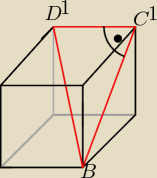
GRANIASTOSŁUPY Anna: Prosiłabym o szczegółowe rozwiązanie tego zadania, abym mogła je przeanalizować, z góry bardzo, bardzo dziękuję ! W prostopadłościanie ABCDA1B1C1D1 podstawa ABCD jest kwadratem. Wysokość C1E trójkąta BC1D1 dzieli przekątną D1B na odcinki długości ; |D1E| = 2 dm |EB| = 8 dm Oblicz objętość tego prostopadłościanu.

Patrick:

pigor: ..., otóż niech dla skrócenia zapisu a − dł. krawędzi podstawy (boku kwadratu), H − dł. wysokości prostopadłościanu i CE₁=h, to V_p=a²H= ? , a z tw. o wysokości względem przeciwprostokątnej Δ BC₁D₁, tw. Pitagorasa i warunków zadania : h²=8*2 i h²=a²−2² i a²+H²+a²=(8+2)² ⇔ ⇔ h²=16 i a²=16+4 i 2a²+H²= 10² ⇒ (**) a²=20 i 40+H²=100 ⇒ ⇒ H²=60=4*15 ⇒ H= 2√15 , stąd z (**) i (*) V_p= 20*2√15= 40√15 odp. V_p= 40√15 dm³ − szukana objętość prostopadłościanu . ...