 Mógłby mnie ktoś naprowadzić na to, jak ugryźć to zadanie?
Wiem, że nie obejdzie się bez zastosowania wzorów na objętości tych brył, ale co z tym dalej
robić?
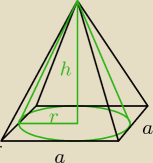
Stożek i ostrosłup prawidłowy czworokątny mają wspólny wierzchołek, a podstawa stożka jest
kołem wpisanym w podstawę ostrosłupa.
Mógłby mnie ktoś naprowadzić na to, jak ugryźć to zadanie?
Wiem, że nie obejdzie się bez zastosowania wzorów na objętości tych brył, ale co z tym dalej
robić?
Stożek i ostrosłup prawidłowy czworokątny mają wspólny wierzchołek, a podstawa stożka jest
kołem wpisanym w podstawę ostrosłupa.
| 1 | ||
a) Oblicz objętość stożka, wiedząc, że objętość ostrosłupa wynosi | V | |
| 3 |




 objętość ostrosłupa
Vo = 13a2*h = 13V
objętość ostrosłupa
Vo = 13a2*h = 13V
| V | ||
a2*h = V → a2 = | ||
| h |
| 1 | V | |||
Vs = | π* | *h
| ||
| 3 | 4h |
| Vπ | ||
Vs = | ||
| 12 |
| 3S − a2 | ||
Pc = a2 + 2a*hs = 3S → hs = | ||
| 2a |
| a | ||
r = | ||
| 2 |
| a | a | 3S−a2 | a | a2 + 3S −a2 | ||||||
Ps = πr(r+l) = π* | ( | + | ) = π | ( | ) =
| |||||
| 2 | 2 | 2a | 2 | 2a |
| a | 3S | 3 | ||||
= π | * | = | π S | |||
| 2 | 2a | 4 |