Planimetria - obliczanie objętości i pola całkowitego Mateusz: Witam, Opuściłem kilka lekcji matematyki i mam teraz problem z wykonaniem dwóch zadan: 1) Pole powierzchni bocznej graniastosłupa prawidłowego trójkątnego wynosi 12√3 cm². Oblicz objętość i pole całości wiedząc, że przekątna ściany bocznej tworzy z wysokością graniastosłupa kąt 60 stopni. 2) W graniastosłupie prawidłowym trójkątnym krawędź podstawy ma długość a i jest 2 razy krótsza od krawędzi bocznej. Wyznacz pole całkowite, objętość i cosinus kąta między przekątną ściany bocznej a sąsiednią ścianą boczną. Co do zadania pierwszego to utknąłem zaraz po wyliczeniu pola pojedynczej ściany bocznej (czyli praktycznie zaraz po starcie). To co mam wygląda następująco: P_pb = 12√3cm² P_b = P_pb:3 = 4√3cm² Narysowany prostokąt dzielę na dwa trójkąty prostokątne, ale niestety tutaj grzęznę. Prosiłbym o "łopatologię" przy tłumaczeniu bo jestem uczniem bardziej dwójkowym niż trójkowym. Pomocy.

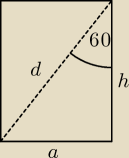
Mateusz: Wiem, że na 100% trzeba tu użyć funkcji trygonometrycznych jednak co z tego, jak nie wiem co dalej?

Godzio:

	a√3
h =
	3

P_b = 3* ah = 12√3 ⇒ 3a² = 36 ⇒ a = 2√3

	a2√3		12√3		6
V =		* h =		*		= 6√3
	4		4		3

heh, i pomyśleć że nie jestem w stanie pisać

Mateusz: Możesz nazwać mnie kretynem ale na nic zda się Twoje rozwiązanie bez wyjaśnień...