a
Tritan:
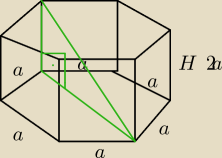
Dany jest graniastosłup prawidłowy sześciokątny, którego krawędź boczna jest dwa razy dłuższa
niż krawędź podstawy. Wyznacz sinus kąta nachylenia najdłuższej przekątnej graniastosłupa do
płaszczyzny jego podstawy.
Zrobiłem rysunek
13 lis 21:24
zosia: będzie 45
o bo trójkąt jest równoramienny
d
2=8a
2d=2a
√2
13 lis 21:34
Tritan: d2=8a2d=2a√2
Hmm, nie rozumiem..
13 lis 21:42
zosia: przekątna podstawy ma długość 2a stądz Pit. (2a)2+(2a)2=d2
d→przekątna graniastosłupa
pomiędzy a2 a d powinien być odstęp były w róznych linijkach,nie wiem dlaczego edytor to
zmienił
13 lis 23:51
Tritan: Dobija mnie ta matma.. Dlaczego jest (2a)2+(2a)2? Ponieważ jest równoramienny? Chryste,
wylewu można dostać.
14 lis 00:04
kylo1303: to z twierdzenia pitagorasa: a2+b2=c2, a ze trojkat jest rownoramienny to a=b
14 lis 00:05
Tritan: To jest co najmniej chore.
Dzięki za pomoc, zrozumiałem.
14 lis 00:06
Tritan: | | 2a | |
Drugi człon zadania też nie zrozumiały.. jakim cudem 2a√2 przekształciliśmy na: |
| |
| | 2a√2 | |
?
14 lis 00:08
kylo1303: To juz jest cos innego. Przeciwprostokatna w twoim trojkacie (oznaczona litera d) wynosi
2a
√2.
Sinusem kata w trojkacie prostokatnym nazywamy stosunek:
1) boku lezacego na przeciwko danego kata
oraz
2) przeciwprostokatna
| | 2a | |
czyli sinα= |
| , gdzie 2a− bok na przeciwko kata, 2a√2− przeciwprostokatna
|
| | 2a√2 | |
skracasz i wychodzi. Staralem sie jak najjasniej potrafie.
14 lis 00:18
Tritan: Mistrz !
Dziękuje. o/
14 lis 00:21