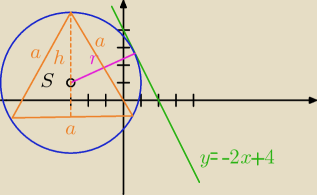
planimetria J: Napisz równanie okręgu o środku w punkcie S=(−3,1) stycznego do prostej: y=−2x+4 oraz oblicz długość boku trójkąta równobocznego wpisanego w ten okrąg.

dero2005:

	|Axs + Bys +C|
r =
	√A2 +B2

y = −2x+4 2x + y − 4 = 0 A = 2 B = 1 C = −4 x_s = −3 y_s = 1

	9
r =		√5
	5

(x−a)² + (y−b)² = r² (x+3)² + (y−1)² = ⁸¹₅ r = ²₃h = ⁹₅√5 h = ²⁷₁₀√5 a = ²₃√3h = ⁹₅√15

J: Dzięki za rozwiązanie