pole Monika: Mając podane punkty: A(−2;2); B(2; −1); C(4; 2); D(2; 5) oblicz pole tego czworokąta. Odpowiedź to 8. Z góry dziękuje za pomoc.

len: narysuj wykres, znajdz te punkty i polacz. a wszystko stanie sie jasne

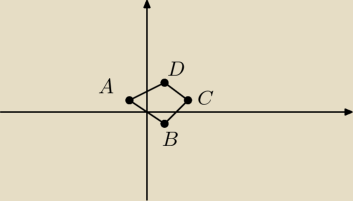
Monika: To nawet mi żadnego kwadratu, trapezu nie przypomina. Jakieś wskazówki co to za czworokąt?

Uczen: Trapez

Monika: A co tu jest podstawami i wysokością?

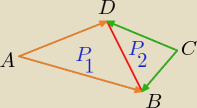
Eta: P= P₁+P₂ → AB=[4,−3]

	1		1
→ P1=		| 4*3−4*(−3)|=		*24= 12
	2		2

AD=[4,3] → CD=[−2,3]

	1		1
→ P2=		*| (−2)*(−3) −3*(−2)|=		*12= 6
	2		2

CB=[−2, −3] Odp: P= 18 [j²] ( a Ty podajesz ,że odp; to 8 ? −−− to nie jest prawdą

Eta: https://matematykaszkolna.pl/forum/forum.py?komentarzdo=i18 Poczytaj komentarz podany przez Gustlika

dero2005: P_ABC = ¹₂|det(BA^→BC^→)| P_ADC = ¹₂|det(DA^→DC^→)| P = P_ABC + P_ADC BA^→ = [−4, 3] BC^→ = [2, 3] |det(BA^→BC^→)| = |−4*3 − [2*3]| = |−12 − 6| = |−18| = 18

	18
PABC =		= 9
	2

DA^→ = [−4, −3] DC^→ = [2, −3] |det(DA^→DC^→)| = |−4*(−3) − [2*(−3)]| = |12 + 6| = |18| = 18

	18
PADC =		= 9
	2

P = 9 + 9 = 18

Monika: A jest jakaś metoda inna, bardziej szkolna?

Eta: To najprostsza metoda .... też "szkolna"

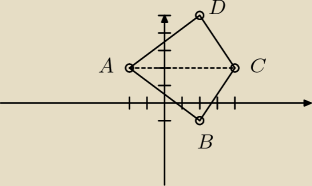
zosia: metoda szkolna "podstawówkowa" Mamy dwa trójkąty o podstawie 6 jednostek i wysokościach 3 jednostki

	1
P=2*		6*3=18
	2

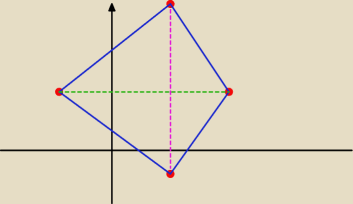
Eta: No tak! ...... ( nie umieszczałam tego czworokąta w układzie współrzędnych Przekątne długości e= f= 6 i są prostopadłe

	e*f		6*6
P=		=		= 18
	2		2

Metoda iście .. "podstawówkowa"

Eta: @ dero No to się "rozpędziliśmy" jak mawia Gustlik metodą : "dookoła świata"

dero2005: Eta ja liczyłem metodą uniwersalną a nie do konkretnego przypadku.

Gustlik: @ Eta, dero Szczerze mówiąc też bym tak policzył, bo metoda "wektorowa" to najprostsza metoda obliczania pól figur w układzie współrzędnych. To właśnie "szkolne" metody obliczania pól są dookoła świata, gdzie wykonuje się żmudne obliczenie odcinków.