Dla jakich wartości parametru m równanie ma dwa różne... izuniaa: Dla jakich wartości parametru m równanie ma dwa różne rozwiązania rzeczywiste ujemne ? x²−2(m+3)x+m²−1=0

alex: Δ>0 x₁*x₂ > 0 czyli m²−1>0 x₁+x₂<0 czyli 2(m+3)<0

izuniaa: A dałbys rade rozwiazac ?

alex: Δ= (−2m−6)²−4(m²−1)= 4m²+24m+36−4m²+4= 24m+40 = 8(3m+5)

	5
Δ>0 ⇒ 3m+5>0 ⇒ m> −
	3

cdn

alex: m²>1 ⇒ m ∊ (−∞,−1) ∪ (1, +∞) 2m+6<0⇒m< − 3

alex: i teraz część wspólna

izuniaa: No wlanie, tylko w odpowiedziach jest ze dla parametru m nie istnieje zadna watrosc...

izuniaa: ?

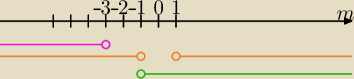
Nela: Alex napisał, że m>−(5/3) (zielony na rysunku) i m ∊ (−∞,−1) ∪ (1, +∞) (pomarańczowy na rysunku) i m< − ( różowy na rysunku) Jak widać te trzy przedziały nie mają części wspólnej, więc nie istnieje żadna wartość dla której spełnione są warunki zadania

chichi: Na rysunku zielony reprezentuje nierówność m > −1