funkcja i logarytmy
Ania: Określ dziedzinę funkcji: LOGARYTMY Proszę o pomoc

a) f(x) = log
3 X
b) f(x) = log
5 (2x + 1)
c) f(x) = log (x
2 + 3)
d) f(x) = log
(x) (x−1)
e) f(x) = log
2−x (x
2 − 4)
jeśli to nie problem proszę o napisanie jakie własności logarytmu są tu wykorzystane
11 lis 17:24
11 lis 17:25
Ania: dziękuję za te wskazówki, przypomniałam sobie wszystkie własności, jednak w dalszym ciągu nie
wiem jak określić dziedzinę w tych zadaniach...
czy mógłby ktoś zrobić przynajmniej jeden przykład a ja analogicznie będę robić dalej?
11 lis 21:51
sushi_ gg6397228:
wiec na podstawie linku−>ściagi pokaz swoje obliczenia, do kazdego przykladu osobno
11 lis 21:55
Karolina: a) x>0
b) 2x+1>0
c) x2 + 3 >0
d) x>0 x≠1 x−1>0
itd...
11 lis 21:55
Aga: W przykładzie a, b, c
x jest tylko w liczbie logarytmowanej, a liczba logarytmowana musi być większa od 0.
Więc rozwiązujesz nierówności.
a)x>0
b) 2x+1>0
c) x2+3>0
Rozwiąż to sprawdzę i dalszych udzielę Ci wskazówek.
11 lis 21:59
Ania: Ok dziękuję bardzo

a) D = ( 0 , +
∞)
b) D = (−
12 , +
∞)
c) D = R
d) D = (1, +
∞)
e) D = (−2, 2) − {1}
Czy to o to chodzi?
11 lis 23:05
sushi_ gg6397228:
a gdzie zalozenia dla podstawy
e) 2−x >0 i 2−x ≠1 i x2−4 >0 kolor czerwony to argument
11 lis 23:09
sushi_ gg6397228:
a,b,c) dobrze
d) zafarciło sie i tez jest OK
x>0 i x≠ 1 i x−1>0
11 lis 23:10
Ania:
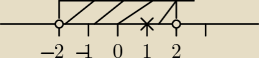
ok dzięki, jeszcze mam pytanie co do tego ostatniego podpunktu
wyszło mi że:
2 − x > 0
x < 2
i
2 − x ≠ 1
x ≠ 1
i
x
2 − 4 >0
x > 2 ∨ x > −2
i narysowałam sobie do tego oś. Z tego mi wyszło że D = (−2, 2 ) − {1}
Czy to jest poprawnie?
11 lis 23:24
sushi_ gg6397228:
x2−4>0 <==> x < − 2 i x > 2
11 lis 23:34
 a) f(x) = log3 X
b) f(x) = log5 (2x + 1)
c) f(x) = log (x2 + 3)
d) f(x) = log(x) (x−1)
e) f(x) = log2−x (x2 − 4)
jeśli to nie problem proszę o napisanie jakie własności logarytmu są tu wykorzystane
a) f(x) = log3 X
b) f(x) = log5 (2x + 1)
c) f(x) = log (x2 + 3)
d) f(x) = log(x) (x−1)
e) f(x) = log2−x (x2 − 4)
jeśli to nie problem proszę o napisanie jakie własności logarytmu są tu wykorzystane
 a) D = ( 0 , +∞)
b) D = (− 12 , +∞)
c) D = R
d) D = (1, +∞)
e) D = (−2, 2) − {1}
Czy to o to chodzi?
a) D = ( 0 , +∞)
b) D = (− 12 , +∞)
c) D = R
d) D = (1, +∞)
e) D = (−2, 2) − {1}
Czy to o to chodzi?
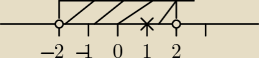 ok dzięki, jeszcze mam pytanie co do tego ostatniego podpunktu
wyszło mi że:
2 − x > 0
x < 2
i
2 − x ≠ 1
x ≠ 1
i
x2 − 4 >0
x > 2 ∨ x > −2
i narysowałam sobie do tego oś. Z tego mi wyszło że D = (−2, 2 ) − {1}
Czy to jest poprawnie?
ok dzięki, jeszcze mam pytanie co do tego ostatniego podpunktu
wyszło mi że:
2 − x > 0
x < 2
i
2 − x ≠ 1
x ≠ 1
i
x2 − 4 >0
x > 2 ∨ x > −2
i narysowałam sobie do tego oś. Z tego mi wyszło że D = (−2, 2 ) − {1}
Czy to jest poprawnie?