Oblicz objętośc graniastosłupa Majkel: Graniastosłup prawidłowy trójkątny przecięto płaszczyzną, przechodzącą przez środek ciężkości górnej podstawy i krawędź dolnej podstawy, pod kątem 45stopni do dolnej podstawy . Pole otrzymanego przekroju wynosi 5²√6. Oblicz objętość tego graniastosłupa coś mi świta wiem że dzwonią ale nie wiem do końca gdzie

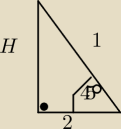
Marcin G.: Pp − pole przekroju H− wysokość graniastosłupa Hp − wysokość przekroju ( na rysunku "1" ) Objętość liczymy ze wzoru −> V = Pp * H Ponieważ jest to trójkąt równoboczny −> Pp = a² √3 /4 Przekrój ma pole 5 √6 = 1/2*a*Hp , więc Hp = 10 √6 /a Środek ciężkości podstawy jest oddalony od boku trójkąta równobocznego o 1/3 wysokości podstawy, więc ten odcinek ma długość a √3 / 6. ( na rysunku "2" ) Z cos45st. liczymy a = 2 √15 Z tan45st. liczymy H = √5 Podstawiamy do wzoru na objętość i mamy V = 15 √15