Proszę o pomoc
Badhead: Proszę o pomoc z tym zadaniem, nie wiem za bardzo jak się do niego zabrać:
Dane jest równanie mx2 − (m − 3)x + 1 = 0 o niewiadomej x. a) wyznacz ZW parametru m, dla
których to równanie ma dwa różne rozwiązania dodatnie b) dla jakich m równanie to ma dwa
rozwiązania x1 i x2 spełniające warunek |x1| + |x2| ≤ 1?
9 lis 15:14
Badhead: Udało mi się rozwiązać to zadanie, a) prawdopodobnie ZWf to m∊(9;+∞), natomiast b) m≥3/2, czyli
odp m>9 ( ze względu na ZWf).
Natomiast mam problem z kolejnym zadaniem:
Drut dł 20dm podzielono na 2 części, z 1 kawałka drutu zrobiono kwadratową ramkę o boku x[dm],
zaś z drugiego prostokątną, której jeden bok jest o 1 dm dłuższy od drugiego: a) napisz wzór
funkcji P opisującej sumę pól kwadratu i prostokąta ograniczonych ramkami, w zależności od dł.
boku kwadratu, określ dziedzinę funkcji P; b) Wykaż: suma pól kwadratu i prostokąta będzie
najmniejsza, gdy drut zostanie podzielony na pół. Wyznacz wymiary prostokątnej ramki.
Obliczyłem wzór funkcji, który najprawdopodobniej to f(p)=2x2 − 10x + 24 3/4, a dziedzina
funkcji to raczej Dp∊(0;20), natomiast mam problem z drugą częścią zadania, nie mam za bardzo
pomysłu jak to wykazać. Proszę o pomoc.
9 lis 16:50
Aga:
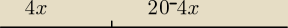
P(x)=2x
2−10x+24,75
4x− obwód kwadratu
20−4x − obwód prostokąta.
x długość bok kwadratu, x>0
4,5−x dł. krótszego boku kwadratu, 4,5−x>0
5,5−x dł dłuższego boku kwadratu, 5,5−x>0
Rozwiązując 3 nierówności i wyznaczając część wspólną otrzymujemy D
P=(0;4,5)
B) jest to funkcja kwadratowa ramionami skierowana do góry, więc przyjmuje wartość najmniejszą
dla x=x
w
| | −b | |
x= |
| =2,5 − bok kwadratu |
| | 2a | |
prostokątna ramka ma wymiary 2dm X 3.dm
obwód kwadratu wynosi 10 i prostokąta też, co należało wykazać
10 lis 21:49
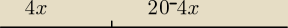 P(x)=2x2−10x+24,75
4x− obwód kwadratu
20−4x − obwód prostokąta.
x długość bok kwadratu, x>0
4,5−x dł. krótszego boku kwadratu, 4,5−x>0
5,5−x dł dłuższego boku kwadratu, 5,5−x>0
Rozwiązując 3 nierówności i wyznaczając część wspólną otrzymujemy DP=(0;4,5)
B) jest to funkcja kwadratowa ramionami skierowana do góry, więc przyjmuje wartość najmniejszą
dla x=xw
P(x)=2x2−10x+24,75
4x− obwód kwadratu
20−4x − obwód prostokąta.
x długość bok kwadratu, x>0
4,5−x dł. krótszego boku kwadratu, 4,5−x>0
5,5−x dł dłuższego boku kwadratu, 5,5−x>0
Rozwiązując 3 nierówności i wyznaczając część wspólną otrzymujemy DP=(0;4,5)
B) jest to funkcja kwadratowa ramionami skierowana do góry, więc przyjmuje wartość najmniejszą
dla x=xw