zlepek funkcji kwadratowych Limbo: Dla jakich wartości parametru m równanie |x²−9|+|x²−16|=m ma dokładnie dwa różne pierwiastki. mam pytanie jaką metodą można najszybciej wykonać zlepek wykresów funkcji |x²−9|+|x²−16| i czy koniecznie trzeba rozpatrywać wszystkie przypadki czy w tym wypadu mogę opuścić wartość bezwzględną bez zmiany znaków następnie odbić to co pod osią OX? Z góry dziękuje za pomoc.

Limbo: poprawka miałem na myśli *następnie narysować wykres 2x²−25 i później odbić to co pod osią \ OX?

Godzio: Niestety nie, trzeba męczyć się z przypadkami

Limbo: :(

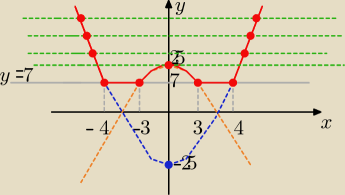
Eta: dla x€ (−∞, −4> U <4,∞) f(x) = x²−9+x²−16= 2x²−25 −−− część paraboli w tych przedziałach dla x€ (−4, −3> U < 3, 4) f(x)= x²−9−x²+16 = 7 −−− części prostej w tych przedziałach dla x€ (−3, 3) f(x)= −x²+9 −x²+16= −2x²+25 −−− część paraboli w tym przedziale odp: dla m > 25 równanie ma 2 różne rozwiązania