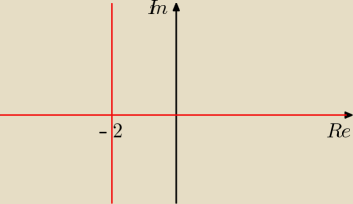
dwa zadania:) ICSP: Na to nie mam pomysłu Wykaż że jeżeli równanie x⁴ + px² + q ma 4 różne rozwiązania rzeczywiste tworzące ciąg arytmetyczny to 9p² = 100q oraz drugie: Z liczb zespolonych rozwiązać równanie(dla x,y rzeczywistych) (z+2)² = (ź + 2)² ź to sprężenie doszedłem do tego że dla y = 0 jest spełnione dla każdej liczby rzeczywistej x oraz dla x = −2 jest spełnione dla każdej liczby y

Aga: pierwiastki: a,a+r, a+2r. a+3r wielomian da się zapisać (x−a((x−a−r)(x−a−2r)(x−a−3r)=x⁴+px²+q Próbowałeś tak robić?

ICSP: hmm nie. Już próbuję.

ICSP: ale to chyba jest bez sensu. Wymnożenie zajmie zbyt dużo czasu. Zaczynam myśleć że jakoś trzeba użyć wzorów Viet'a. Jednak nie mam pomysłu jak to zrobić po podstawieniu.

xXx: odnosnie drugiego to wg mnie to co napisales jest calym rowiazaniem

ICSP: mi też się tak włąśnie zdaje Mogłem gdzieś zgubić rozwiązanie. Teraz meczę się z tym: Mam policzyć moduł liczby zespolonej:

	π		π
1 + itgα gdzie α∊ (−		;		)
	2		2

	1
wychodzi :		i czy to jest dobry wynik?
	cosα

Oczywiście dziękuje za drugie

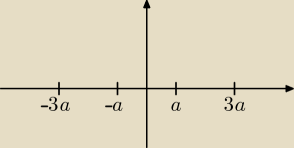
Bogdan: (x + 3a)(x + a)(x − a)(x − 3a) = 0 (x² − 9a²)(x² − a²) = 0 x⁴ − 10a²x² + 9a⁴ = 0 p = −10a², 9p² = 900a⁴ q = 9a⁴, 100q = 900a⁴ Mam nadzieję, że idea rozwiązania jest czytelna.

ICSP: oczywiście że jest czytelna Też brałem pod uwagę liczby −3,−1,1,3 sądząc że to jedyny możliwy ciąg. Zapomniałem jednak o tej literce a Dziękuję bardzo

Bogdan:

ICSP: a można jeszcze jakoś udowodnić że tylko liczby −3a −a a 3a spełniają warunki zadania?

Bogdan: Jeśli wielomian W(x) = ax⁴ + bx² + c ma cztery różne miejsca zerowe, to jak układają się one na osi x ?

ICSP: wtedy funkcja jest parzysta czyli jeżeli x₂ = −x₁

Bogdan: Ciepło, ciepło

Eta: x²= t, t>0 Δ>0 x= −√t₁ v x= −√t₂ v x= √t₂ v x= √t₁ z def. ciągu otrzymasz t₁= 9t₂ ze wzorów Viete^'a t₁+t₂= −p >0 t₁*t₂= q >0 wystarczy? ......... dokończ

ICSP: a z tym zadaniem z modułem możecie jeszcze pomóc?

Godzio: Jakim

ICSP: z 20:46. Tuż przed pierwszym postem Bogdana.

Godzio: To nawet nie musiałeś pytać, zadanie jest oczywiste i oczywiście masz dobry wynik

ICSP: Myślałem ze skoro taki dziwny wynik to źle Dziękuję bardzo

Eta:

ICSP: Odpocznę godzinkę i chyba zabiorę się za najtrudniejsze zadanie na kartce

Godzio: Jak byś miał trudne z zespolonych + wielomiany jakaś taka mieszanka to pisz, jutro mam algebrę to akurat bym sobie coś pyknął