 Skoro najmniejsza wartośc wynosi 1 to
1) Δ>0
2) m−1>0
3) q=c−ap2
c−ap2=1
1) Δ=(m−2)2−4(m−1)*1
Δ=m2−4m+4−4m+4>0
m2−8m+8>0
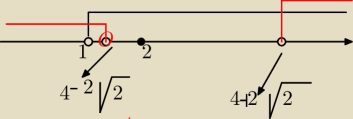
m1=4−2√2≈1,17
m2=4+2√2≈6,83
m∊(−∞,4−2√2)U(4+2√2,∞)
2)m−1>0
m>1
Skoro najmniejsza wartośc wynosi 1 to
1) Δ>0
2) m−1>0
3) q=c−ap2
c−ap2=1
1) Δ=(m−2)2−4(m−1)*1
Δ=m2−4m+4−4m+4>0
m2−8m+8>0
m1=4−2√2≈1,17
m2=4+2√2≈6,83
m∊(−∞,4−2√2)U(4+2√2,∞)
2)m−1>0
m>1
| (m−2)2 | ||
3) 1−(m−1)* | =1 | |
| 4(m−1)2 |
| (m−2)2 | ||
1− | =1 | |
| 4(m−1) |
| (m−2)2 | ||
− | =0 | |
| 4(m−1) |
 przecież samo stwierdzenie iż te funkcje przyjmują najmniejszą wartość równą 1 mówi, że nie
może przyjąć wartości 0, gdyż 1 jest najmniejszą. warunek z deltą jest sprzeczny z zadaniem
przecież samo stwierdzenie iż te funkcje przyjmują najmniejszą wartość równą 1 mówi, że nie
może przyjąć wartości 0, gdyż 1 jest najmniejszą. warunek z deltą jest sprzeczny z zadaniem 
