rozwiąż równanie marcin: |x+5|−|2x−3|+|2x+4|=34 Witam! mam pytanie...czy przy takim zadaniu muszę tylko rozpisać je na więcej przykładów i rozwiązać jak każde inne z wartością bezwzględną

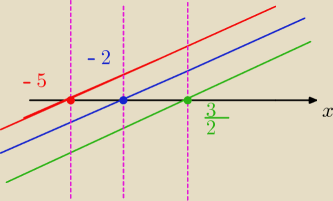
Limbo: miejsca zerowe dla x+5 funkcja liniowa rosnąca bo współczynnik przy x=1 czyli a>0, "a" to współ.kierunkowy i od tego zależy czy funkcja liniowa jest rosnąca, malejąca czy stała. x₀=−5 dla 2x−3 rosnąca rosnąca bo współczynnik przy x równa się 2 czyli a>0

	3
x0=
	2

dla 2x+4 rosnąca bo .... x₀=−2 robisz uproszczony rysunek funkcji liniowych (tzn broń boże nie rób dokładnych wykresów bo chodzi tylko o to czy funkcja jest dodatnia czy nie w danym przedziale i kiedy jest pod osią x to trzeba przy opuszczaniu zmienić jej znak, jak jest nad osią opuszczasz bez zmiany znaku)

	3		3
widzisz przedziały od (−∞;−5) później od <−5;−2) później od <−2;		) później od <		;∞)
	2		2

i patrzysz w którym przedziale funkcja jest pod osią x jak któraś jest pod osią x to zmieniasz jej znak zgodnie z definicją wartości bezwzględnej w przedziale od (−∞;−5) wszystkie są ujemne więc wszystkim wartością bezwzględnym zmieniasz znak. opuść z zmianą znaku wszystkie wartości |x+5|−|2x−3|+|2x+4|=34 w przedziale <−5;−2) opuszczając zmieniasz znaki niebieskiej i zielonej funkcji liniowej a czerwoną opuszczasz bez zmian itd rozpatrujesz przypadki.

Limbo: https://matematykaszkolna.pl/strona/41.html

marcin: dzięki wielkie tak właśnie zrobiłem

Limbo: tak najprościej na tej stronce trochę brak tych rysunków przy wartościach bezwzględnych i gorzej to widać, rób rysunki i stosuj tą metodę chyba najszybciej jest