zzzzzz natalia: w trójkąt równoramienny o kącie rozwartym 120 stopni wpisano okrąg o promieniu 5 cm. oblicz obwód i pole tego trójkąta

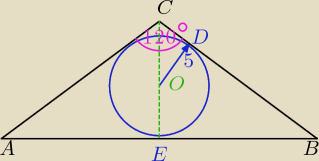
dero2005: |OD| = |OE| = 5

|OD|		√3
	= sin 60o =
|OC|		2

|OC| = |EC| = |OE| + |OC|

|EB|
	= tg 60o = √3
|EC|

|EB| = P = |EB|*|EC| =

|EB|		√3
	= sin 60o =
|BC|		2

|BC| = Obwód = 2(|EB| + |BC|) =

natalia: mógł by mi to ktoś rozwiązać całkiem i wytłumaczyć czemu tak , bo jestem całkiem nie rozumiem..... błagam .

dero2005:

	2|OD|		2*5		10√3
|OC| =		=		=
	√3		√3		3

	10√3		15 + 10√3
|EC| = |OE| + |OC| = 5 +		=
	3		3

|EB| = |EC|√3 = 5√3 + 10

	15 + 10√3		175√3+300
P = |EB|*|EC| = (5√3 + 10)		=
	3		3

	2√3*|EB|		2√3(5√3+10)		30+20√3
|BC| =		=		=
	3		3		3

	30+20√3		70√3+120
Obwód = 2(EB|+|BC|) = 2[(5√3+10) +		] =
	3		3

dero2005: trójkąt Δ_ODC jest prostokątny o boku OD = 5 i kącie OCD = 60^o. Z zależności trygonometrycznych liczymy bok (odcinek) OC. Suma odcinków OC i OE stanowią odcinek EC (wysokość trójkata). Rozpatrujemy teraz trójkąt Δ_EBC. Stosunek boków EB do BC stanowi tangens kąta 60^o (ECB). Z tej zależności liczymy odcinek EB. Iloczyn odcinka EB i EC jest polem trójkąta. Stosunek odcinka EB do BC stanowi sinus kąta 60^o (ECB). Z tej zależności liczymy długość odcinka BC. Suma odcinka BC i BE stanowi połowę obwodu. Po pomnożeniu przez 2 mamy cały obwód.

Sylwia:

	15 + 10√3
Wiem, że to powinnam wiedzieć ale dlaczego z (5√3 + 10)		wychodzi wynik
	3

	175√3 + 300
		?
	3