nierówność logarytmiczna gryps: log(x²−9) > log(4−x²) +2

gryps: proszę o pomoc

Bogdan: Podaj najpierw założenia

gryps: x²−9>0 x=3 x=−3 4−x²>0 x=2 x=−2 co dalej?

konrad: to są nierówności, zatem rozwiązaniem są przedziały

gryps: Zostawmy założenia, co z nierównością?

gryps: tyle to wiem, ale co dalej coś przerzucamy ? co z tą dwójką po prawej stronie robimy

konrad: spójrz sobie na ten przykład https://matematykaszkolna.pl/strona/254.html

Bogdan: Najpierw wyznaczyć trzeba założenia.

gryps: to wiem, co zrobić jak już opuszczę logarytmy?

konrad: Spojrzałem na przykład?

konrad: *łeś

gryps: tak, tam jest dzielenie nawiasów, żeby usunąć dół mnożę przez mianownik normalny czy do potęgi2?

gryps: po prostu mam problem z nierównością

Bogdan: Po określeniu założeń pogadamy co zrobić dalej.

konrad: Normalny, bo z założenia wynika, że (4−x²) musi być większe od zera.

Eta: D= .... wystarczy? dlatego Bogdan przypominał : "podaj założenia" !

Eta: Przepraszam Bogdanie, że się wcięłam . Obiecuję poprawę

gryps: Ja też, będę większą uwagę zwracać na założenia, dzięki.

Bogdan: Eto wcinaj się, wcinaj , nie gniewam się. Mam jednak wątpliwość do rysowania strzałek, szczególnie w lewą stronę przy rysowaniu przedziałów.

Martyna18: (4−x²) mozna tak rozumować? −(b−a)(a+b)= −(x−2)(x+2) ten minus ma oznaczac ze f malejąca.

Eta: Hmm .... wytłumacz mi co z tymi "strzałkami" ?

Martyna18: ?

konrad: (4−x²)=−(x²−4)=−(x−2)(x+2) minus oznacza, że ramiona paraboli są skierowane w doł, nie że funkcja jest malejąca

Martyna18: dzieki

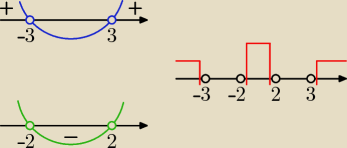
Bogdan: Założenia: (1) x² − 9 > 0 ⇒ (x − 3)(x + 3) > 0 (2) 4 − x² > 0 ⇒ x² − 4 < 0 ⇒ (x − 2)(x + 2) < 0 Częścią wspólną rozwiązań nierówności (1) i (2) jest zbiór pusty, a to oznacza, że nierówność nie zachodzi dla żadnej liczby x. Odp.: x∊∅

Bogdan: Eto, mój adres mailowy na potrzeby tego forum to: matura@vp.pl. Prześlij mi na moją pocztę swój adres, chciałbym od czasu do czasu zamienić z Tobą kilka słów , bardzo proszę.