Rozwiąż Sonia19: Rozwiąż równanie: |x+2|+|x−1|=10 x+2+x+1=10 2x=9 x=4.5 −x−2−x+1=10 −2x=11 x=−5.5 Dobrze to robię?

Eta: Niestety źle

Sonia19: a co jest źle?:(

Sonia19: założenia wartość bezwględna większa od 0 x+2>0 x>−2 x−1>0 x>1 A co dalej?

Eta: I I I I II I III −−−−−−−−− −2−−−−−−−−−−−− 1−−−−− I / dla € (−∞, −2) −x−2−x+1= 10 II / dla x€ <−2, 1) x+2 −x+1=10 III / dla x€ <1, ∞) x+2+x−1=10 każde z rozwiązań musi należeć do danego przedziału

Sonia19: Proszę o pomoc:(

Eta: https://matematykaszkolna.pl/strona/1796.html

Sonia19: Jeśli nie należy to co piszemy?

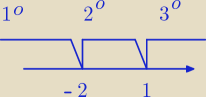
rumpek: |x+2|+|x−1|=10 1. Wypisuję miejsca zerowe: x_o = −2; x_o = 1 2. Układam przedziały: 1^o x∊(−∞;−2) 2^o x∊<−2,1) 3^o x∊<1,+∞) 3. Opuszczam przedziałami znak wartości bezwzględnej. Dla 1^o x∊(−∞;−2) −(x + 2) − (x − 1) = 10 −x − 2 − x + 1 = 10 −2x − 1 = 10 −2x = 11 / : (−2)

	11
x = −		= − 5,5 ∊ (−∞;−2)
	2

Reszta podobnie

Sonia19: Nie wiek skad ten przedział 1^o x∊(−∞;−2)

Sonia19: nie wiem* help:(

Sonia19: Pomóżcie nie wiem skad wzial sie ten pierwszy przedzial tylko o to mi chodzi

Sonia19: 1^o x∊(−∞;−2) dlaczego jest taki przedział?

Eta: Liczysz miejsca zerowe pod modułami x+2=0 => x = −2 i x−1=0 => x= 1 i rozpatrujesz przedziały na osi liczbowej na lewo od −2 czyli (−∞, −2) itd... tak jak zaznaczył Ci rumpek na rysunku

Sonia19: dzieki

Sonia19: 2^o −x−2+x−1=10 −3=10? i co z tym?

Eta: sprzeczność ... czyli brak rozwiązania w tym przedziale

fefefefe: 2|x−4|+|3x−12|<4+|8−2x|

jc: |x+2|+|x−1|=10 Odległość pomiędzy −2 a 1 wynosi 3. Pomyśl, że przyczepiasz sznurek o długości 10 do punktów −2 i 1. Dokąd sięga po naciągnięciu? (10−3)/2 = 3,5 Szukane punkty: 1 + 3,5 = 4,5 oraz −2−3,5=−5,5.

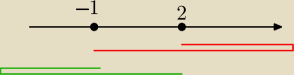
jc: Tu masz rysunek.

jc: Oj, pomyliłem liczby (2 zamieniłem z 1), ale to nie ma znaczenia.

jskbdd: 2x2−(2x+1)(x−2)=5 {tam na początku po 2 jest do kwadratu jak cos)