Dla jakich wartości parametru m równanie ma 2 różne rozwiązania ? mati: mx²−(2m−1)x+2m−1=0

Aga: m≠0 Δ>0

mati: No tak, ale czy mógłby ktoś mi ten jeden przykład rozwiązać krok po kroku?

Aga: Δ=b²−4ac=[−(2m−1)]²−4*m(2m−1)=−4m²+1 −4m²+1>0

	1		1
m1=−		m2=
	2		2

	1		1
m∊(−		;		) i m≠0.
	2		2

rumpek: 1^o Gdy m = 0 0*x² − (2*0 − 1)x + 2*0 − 1 = 0 −(−1)x −1 = 0 x − 1 = 0 x = 1 To mamy tylko jeden pierwiastek, także założenie m ≠ 0 2^o

⎧	Δ>0
⎩	m≠0

Δ = (2m − 1)² − 4 * m * (2m − 1) = (4m² − 4m + 1) − (4m * (2m − 1)) = = 4m² − 4m + 1 − 8m² + 4m = −4m² + 1 −4m² + 1 > 0 / * (−1) 4m² − 1 < 0 / : 4

	1
m2 −		< 0
	4

	1		1
(m −		)(m +		) < 0
	2		2

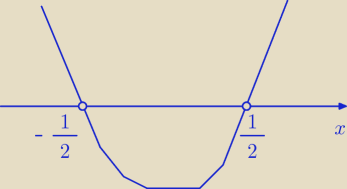
Teraz rysujesz parabolkę odczytujesz (uwzglęniasz, że nie może być m = 0)

	1		1
Już tak na szybko narysowałem i teoretycznie odp. to: m∊(−		, 0)U(0,		)
	2		2

I przed wszystkim sprawdź czy się zgadzają obliczenia bo coś ostatnio za dużo błędów robię xD

mati: Dzieki wielkie