wykres funkcji grochu82: Naszkicuj wykres funkcji, która jest określona dla każdej liczby x∈<−9;9> oraz dla argumentu −3 przyjmuje wartość 5, a dla argumentu 3 wartosc −5, najwieksza wartość tej funkcji to 7, a najmiejsza −6. Funkcja ma 3 miejsca zerowe i nie przyjmuje wartości 2 .

paweł: paweł

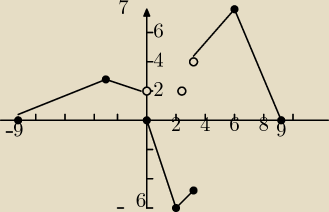
Aga: To puste kółeczko na (2,2) jest niepotrzebne. Wykresów spełniających te warunki można narysować wiele.

grochu82: W jaki sposób można rozwiązać takie zadanie i jakie są wzory tych funkcji?

Aga: Wydaje się, że nie ma w poleceniu , by podać wzór funkcji. Wykres jednak trzeba poprawić, bo ta funkcja przyjmuje wartość 2. To kółeczko puste przenieś na (−4,2) i zaznacz np kropką punkt (−4,−1)

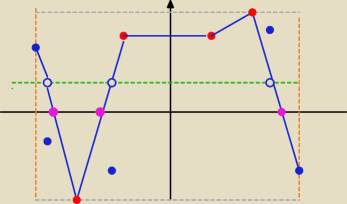
Aga: Musisz zaznaczyć punkty które należą do wykresu: (−3,5) i(3,−5) dziedzina<−9,9> rysujesz pomocnicze linie przerywane leżące na prostej x=−9 i x=9 . Od jednej prostej zaczynasz, a kończysz na drugiej kółeczkami zamalowanymi. Rysujesz poziome linie pomocnicze (największa to 7)czyli y=7, najmniejsza to −6 (rysujesz linię poziomą przechodzącą na y przez −6) Dalej uwzględniasz, że ma być 3 miejsca zerowe, czyli trzy punkty muszą należeć do osi x. I ostatni warunek na prostej y=2 muszą być kółeczka puste , a pod nim gdzieś zamalowane. Pierwszy wykres ma jeszcze jeden błąd ,bo nie (−3,3). tylko (−3,5) ma należeć do wykresu. Napisz, czy zrozumiałeś.

grochu82: Dziękuje za szczegółowe wyjaśnienie teraz wszystko jasne pozdrawiam.