rozwiąż nierówność Jaro: 2+(3/(x+1))>2/x

Jaro: rozwiąż nierówność 2+(3/(x+1))>2/x proszę o pomoc

Dorotaz: ja bym zrobiła tak:

	3		2
2+		−		>0
	x+1		x

2(x+1)x+3x−2(x+1)
	>0 dziedzina Df = R \ {−1,0}
(x+1)x

2(x+1)x+3x−2(x+1)>0 2x²+2x+3x−2x−2 >0 2x² +3x − 2 > 0 Δ = 9 + 16 = 25 pierwiastek z delty = 5

	−3−5		−8
x1 =		=		= −2
	2*2		4

	−3+5		2		1
x2 =		=		=
	2*2		4		2

odp: x ∊(−∞,−2) ∪ (1/2, +∞) ponieważ funkcja ma ramiona paraboli do góry to wartości większe od zera nie wiem czy coś nie pokręciłam, ale powinno być dobrze

lenka: niedobrze, nie wolno mnożyc nierówności przez mianownik, nie robiac założenia, należy pomnożyc przez mianownik² lub tzw. zamienic iloraz na iloczyn czyli od trzeciej linijki powinno byc: [2(x+10)x+3x−2(x+1)]*(x+1)*x>0

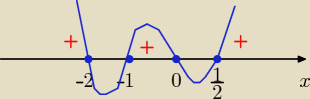
Eta: D= R\{−1,0} po przekształceniach :

	1
2x(x−		)(x+2)(x+1)>0
	2

	1
x€ (−∞, −2) U ( −1, 0) U (		, ∞)
	2