: stożek o objętości V przecięto płaszczyzną równoległą do podstawy przechodzącą mila: : stożek o objętości V przecięto płaszczyzną równoległą do podstawy przechodzącą przez środek wysokości objętość przeciętego w ten sposób stożka jest równa.zapisz obliczenia

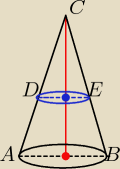
Eta: ΔABC ~ΔDEC w skali k= 2

	V(st.ABC)
to		= k3= 8
	V(st. DEC)

	1
V(st. DEC)=		V(st.ABC)
	8

	7
V(st. ściętego ABDE)=		V(st. ABC)
	8